题目内容
如图,在直角梯形纸片 中,
中, ,
, ,
, ,将纸片沿过点
,将纸片沿过点 的直线折叠,使点
的直线折叠,使点 落在边
落在边 上的点
上的点 处,折痕为
处,折痕为 .连接
.连接 并展开纸片.
并展开纸片.
(1)求证:四边形 是正方形;
是正方形;
(2)取线段 的中点
的中点 ,连接
,连接 ,如果
,如果 ,试说明四边形
,试说明四边形 是等腰梯形.
是等腰梯形.

【答案】
(1)∵ ,
, ,
, .
.
由沿 折叠后
折叠后 与
与 重合,知
重合,知 ,
, .
.

 四边形
四边形 是矩形,且邻边
是矩形,且邻边 相等.
相等.
 四边形
四边形 是正方形.
是正方形.
(2)∵ ,且
,且 ,
, 四边形
四边形 是梯形.
是梯形.
∵四边形 是正方形,
是正方形, ,
, .
.
又点 为
为 的中点,
的中点, .连接
.连接 .
.
在 与
与 中,∵
中,∵ ,
, ,
, ,
,
 ,
, .
.
∵ ,
, ,
, 四边形
四边形 是平行四边形.
是平行四边形.
 .
. .
. .
.
 四边形
四边形 是等腰梯形.
是等腰梯形.
【解析】(1)因为折叠以为着全等,所以AD=DE, .易证四边形AFED是正方形;(2)连接DG由于BG与CD平行且相等,所以四边形BCDG是平行四边形.∴
.易证四边形AFED是正方形;(2)连接DG由于BG与CD平行且相等,所以四边形BCDG是平行四边形.∴ .在正方形AFED中,易证△DAG≌△EFG,从而
.在正方形AFED中,易证△DAG≌△EFG,从而 ,故
,故 ,故四边形GBCE是等腰梯形.
,故四边形GBCE是等腰梯形.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,在直角梯形纸片ABCD中,AD∥BC,∠ABC=90°,将纸片沿过点A的直线折叠,使点B与点D重合,折痕为AG.连接DG并展开纸片.
如图,在直角梯形纸片ABCD中,AD∥BC,∠ABC=90°,将纸片沿过点A的直线折叠,使点B与点D重合,折痕为AG.连接DG并展开纸片. 如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上的一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为
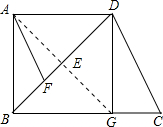
如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上的一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为 如图,在直角梯形纸片ABCD中,AB∥DC,∠A=90°,CD>AD,将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为DF.连接EF并展开纸片.
如图,在直角梯形纸片ABCD中,AB∥DC,∠A=90°,CD>AD,将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为DF.连接EF并展开纸片.
