题目内容
如图，在直角梯形纸片ABCD中，AD∥BC，∠A=90°，∠C=30°，点F是CD边上的一点，将纸片沿BF折叠，点C落在E点，使直线BE经过点D，若BF=CF=8，则AD的长为2
| 3 |
2
．| 3 |
分析：利用等边对等角可以得到∠FBC=∠C=30°，再利用折叠的性质可以得到∠EBF=∠CBF=30°，从而可以求得∠BDF=90°．即可求得线段BD的长，然后在直角三角形ABD中求得AD即可．
解答：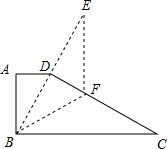
解：如图：∵BF=CF=8，
∴∠FBC=∠C=30°，
∵折叠纸片使BC经过点D，点C落在点E处，BF是折痕，
∴∠EBF=∠CBF=30°，
∴∠EBC=60°，
∴∠BDF=90°，
∵BF=CF=8，
∴BD=BF•sin60°=4
，
∵AD∥BC，
∴∠ADB=∠EBC=60°，
∵∠A=90°，
∴AD=BD•cos60°=2
．
故答案为：2
．
解：如图：∵BF=CF=8，∴∠FBC=∠C=30°，
∵折叠纸片使BC经过点D，点C落在点E处，BF是折痕，
∴∠EBF=∠CBF=30°，
∴∠EBC=60°，
∴∠BDF=90°，
∵BF=CF=8，
∴BD=BF•sin60°=4
| 3 |
∵AD∥BC，
∴∠ADB=∠EBC=60°，
∵∠A=90°，
∴AD=BD•cos60°=2
| 3 |
故答案为：2
| 3 |
点评：本题考查了梯形的性质、三角函数、等腰三角形的性质以及折叠的性质．此题难度适中，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．
练习册系列答案
相关题目
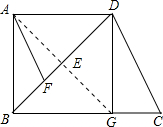如图，在直角梯形纸片ABCD中，AD∥BC，∠ABC=90°，将纸片沿过点A的直线折叠，使点B与点D重合，折痕为AG．连接DG并展开纸片．
如图，在直角梯形纸片ABCD中，AB∥DC，∠A=90°，CD＞AD，将纸片沿过点D的直线折叠，使点A落在边CD上的点E处，折痕为DF．连接EF并展开纸片．
