题目内容
19. 如图,在四边形ABCD中,AD∥BC,E为AB中点,连接DE、CE,CD=AD+BC,则下列结论中①DE⊥CE;②DE平分∠ADC;③CE平分∠DCB;④S△ADE+S△CDE=S△CDE,其中正确的有4个.
如图,在四边形ABCD中,AD∥BC,E为AB中点,连接DE、CE,CD=AD+BC,则下列结论中①DE⊥CE;②DE平分∠ADC;③CE平分∠DCB;④S△ADE+S△CDE=S△CDE,其中正确的有4个.
分析 延长DE交CB的延长线于F,根据平行线的性质得到∠ADE=∠F,通过全等三角形得到AD=BF,DE=EF,根据等腰三角形的性质得到DE⊥CE,∠EDC=∠F,等量代换得到∠ADE=∠CDE,根据全等三角形的性质即可得到结论.
解答 解:延长DE交CB的延长线于F,
∵AD∥BC,
∴∠ADE=∠F,
∵E为AB中点,
∴AE=BE,
在△ADE与△BFE中,$\left\{\begin{array}{l}{∠ADE=∠F}\\{AE=BE}\\{∠AED=∠BEF}\end{array}\right.$,
∴△ADE≌△BEF,
∴AD=BF,DE=EF,
∵CD=AD+BC,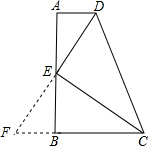
∴CD=CF,
∴DE⊥CE,∠EDC=∠F,
∴∠ADE=∠CDE,
∴DE平分∠ADC,
同理CE平分∠DCB,
∵DE=EF,CE⊥DF,
∴S△CDE=S△CEF=S△ADE+S△BCE.
故正确的有①②③④,
故答案为:4.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
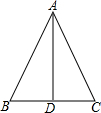 如图,在△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=90°.
如图,在△ABC中,AB=AC,AD是BC边上的中线,则∠BDA=90°.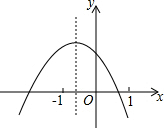 二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)
二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②c>0;③b2-4ac>0;④a+b+c>0.其中正确结论的序号是①②③(把所有正确结论的序号都填在横线上)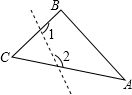 如图,在△ABC中,∠C=40°,若沿图中虚线剪去∠C,则∠1+∠2=120°.
如图,在△ABC中,∠C=40°,若沿图中虚线剪去∠C,则∠1+∠2=120°.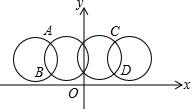 某汽车的标志图案是一个轴对称图形.在如图所示的直角坐标系中,y轴是其对称轴.若点A的坐标是(-3,4),点B的坐标是(-3,1,3),则点C的坐标为(3,4),D的坐标为(3,1.3).
某汽车的标志图案是一个轴对称图形.在如图所示的直角坐标系中,y轴是其对称轴.若点A的坐标是(-3,4),点B的坐标是(-3,1,3),则点C的坐标为(3,4),D的坐标为(3,1.3).