题目内容
12.问题提出:数学课本上有这样一道题目:如图①,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm.把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?初步思考:
(1)试计算出正方形零件的边长;
深入探究:
(2)李华同学通过探究发现如果要把△ABC按照图②加工成三个相同大小的正方形零件,△ABC的边BC与高AD需要满足一定的数量关系.则这一数量关系是:AD=BC.(直接写出结论,不用说明理由);
(3)若△ABC可以按照图③加工成四个大小相同的正方形,且∠B=30°,求证:AB=BC.
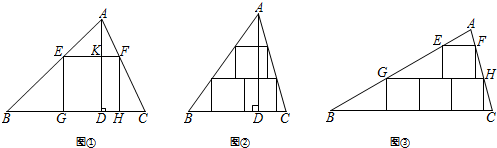
分析 (1)设正方形零件的边长为x mm,则KD=EF=x,AK=80-x,根据EF∥BC,得到△AEF∽△ABC,根据相似三角形的性质得到比例式,解方程即可得到结果;
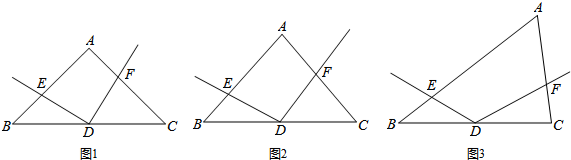
(2)BC=AD,如图2由已知条件得:EF∥GH∥BC,通过△GBN≌△EGM,得到EG=BG,根据△AEF∽△AGH,得到比例式$\frac{AE}{AG}=\frac{EF}{GH}=\frac{1}{2}$,证得AE=EG,于是得到AE=EG=GB,再由△AEF∽△ABC,得到比例式$\frac{AP}{AD}=\frac{EF}{BC}=\frac{AE}{AB}=\frac{1}{3}$,即可得到结论.
(3)如图3,过点A作AD⊥BC于D,分别交EF、GH于点M、N,设每个正方形的边长为a,根据EF∥GH∥BC,推出△AEF∽△AGH∽△ABC,于是得到$\frac{AM}{EF}=\frac{AN}{GH}=\frac{AD}{BC}$,列方程即可得到结论.
解答  解:(1)设正方形零件的边长为x mm,则KD=EF=x,AK=80-x,
解:(1)设正方形零件的边长为x mm,则KD=EF=x,AK=80-x,
∵EF∥BC,
∴△AEF∽△ABC,
∵AD⊥BC,
∴$\frac{EF}{BC}=\frac{AK}{AD}$,
∴$\frac{x}{120}=\frac{80-x}{80}$,
解得x=48.
答:正方形零件的边长为48mm.
(2)BC=AD,
如图2由已知条件得:EF∥GH∥BC,
在△GBN与△EGM中,
$\left\{\begin{array}{l}{∠EGM=∠B}\\{∠EMG=∠GNB}\\{EM=GN}\end{array}\right.$,
∴△GBN≌△EGM,
∴EG=BG,
∵△AEF∽△AGH,
∴$\frac{AE}{AG}=\frac{EF}{GH}=\frac{1}{2}$,
∴AE=EG,
∴AE=EG=GB,
∴△AEF∽△ABC,
∴$\frac{AP}{AD}=\frac{EF}{BC}=\frac{AE}{AB}=\frac{1}{3}$,
∵PD=2x,
∴AD=3x,BC=3x,
∴AD=BC,
故答案为:AD=BC;
(3)如图3,过点A作AD⊥BC于D,分别交EF、GH于点M、N,
设每个正方形的边长为a,
∵EF∥GH∥BC,
∴△AEF∽△AGH∽△ABC,
∴$\frac{AM}{EF}=\frac{AN}{GH}=\frac{AD}{BC}$,
∴$\frac{AD-2a}{a}=\frac{AD-a}{3a}=\frac{AD}{BC}$,
解得AD=2.5a,BC=5a,
∴BC=2AD.
∵∠B=30°,AD⊥BC,
∴AB=2AD,
∴AB=BC.
点评 本题考查了相似三角形的判定和性质,正方形的性质,全等三角形的判定与性质,正确的作出辅助线是解题的关键.

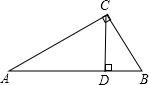 如图,在Rt△ABC中,CD是斜边AB上的高,则图中相似三角形的对数有( )
如图,在Rt△ABC中,CD是斜边AB上的高,则图中相似三角形的对数有( )| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
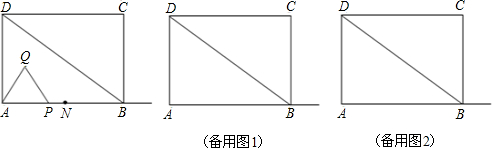
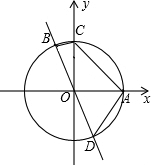 如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为4$\sqrt{2}$.
如图,已知⊙O经过点A(2,0)、C(0,2).直线y=kx(k≠0)与⊙O分别交于点B、D,则四点A、B、C、D组成的四边形面积的最大值为4$\sqrt{2}$.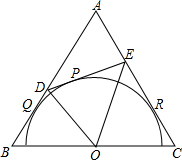 如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.
如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.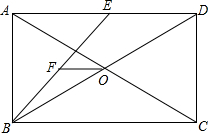 如图所示,E是矩形ABCD的AD的中点,F为BE的中点,△BOF面积为5cm2,求ABCD的面积.
如图所示,E是矩形ABCD的AD的中点,F为BE的中点,△BOF面积为5cm2,求ABCD的面积.