题目内容
【题目】如图,直角坐标系中,直线 y=kx+b 分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).
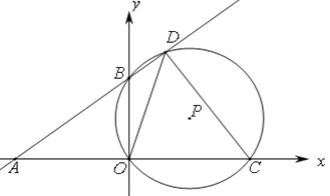
(1)求直线AB的函数表达式.
(2)若点D在第一象限,且tan∠ODC=![]() , 求点D的坐标.
, 求点D的坐标.
(3)当△ODC为等腰三角形时,求出所有符合条件的m的值.
(4)点P,Q关于OD成轴对称,当点Q恰好落在直线AB上时,直接写出此时BQ的长.
【答案】(1)y=![]() x+6;(2)D(
x+6;(2)D( ![]() ,
, ![]() );(3)m的值为-3或
);(3)m的值为-3或![]() 或12或 8;(4)BQ=
或12或 8;(4)BQ=![]() .
.
【解析】
(1)把A、B两点坐标代入y=kx+b求出k、b的值即可;(2)连结BC,作DE⊥OC于点E,根据圆周角定理可得∠OBC=∠ODC,由tan∠ODC=![]() 可求出OC的长,进而可得AC的长,利用∠DAC的三角函数值可求出DE的长,即可得D点纵坐标,代入直线AB解析式求出D点横坐标即可得答案;(3)分四种情况泰伦,利用两点间距离公式及相似三角形对应边成比例列式即可;(4)分析四边形DPOQ为菱形,推出∠BOP=∠ABO,利用三角函数求线段长度;
可求出OC的长,进而可得AC的长,利用∠DAC的三角函数值可求出DE的长,即可得D点纵坐标,代入直线AB解析式求出D点横坐标即可得答案;(3)分四种情况泰伦,利用两点间距离公式及相似三角形对应边成比例列式即可;(4)分析四边形DPOQ为菱形,推出∠BOP=∠ABO,利用三角函数求线段长度;
解:
(1)∵A(-8,0)、B(0,6)在y=kx+b上,
∴![]() ,解得
,解得![]() ,
,
∴直线AB的函数表达式为y=![]() x+6.
x+6.
(2)连结BC,作DE⊥OC于点E,
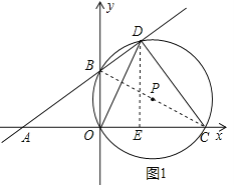
∵∠BOC=90°,
∴BC为⊙P的直径,
∴∠ADC=90°,
∵∠OBC=∠ODC,tan∠ODC=![]() ,
,
∴![]() ,
,
∵OB=6,OA=8,
∴OC=10,AC=18,AB=10,
∵cos∠DAC=![]() =
=![]() ,sin∠DAC=
,sin∠DAC=![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
令 ![]() ,
,![]() ,
,![]() ,
,
∴D( ![]() ,
,![]() )
)
(3)①如图2所示,当DC=OC时,

∵BC=BC,∠BDC=∠BOC=90°,
∴△BDC≌△BOC(HL),
∴BD=BO=6,
设点D的坐标为(n,![]() ),
),
∴BD=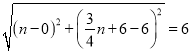 ,
,
解得n=![]() ,
,
∴D(![]() ,
,![]() ),
),
∵C(m,0),
∴DC= ,
,
解得m=-3.
②如图3所示,当OD=DC时,
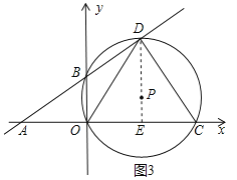
过D作DE⊥OC于点E,
设点D的坐标为(a,![]() ),则m=2a,
),则m=2a,
∴DE=![]() , EC=a,AE=8+a,
, EC=a,AE=8+a,
∴△ADE∽△DCE,
∴![]() ,
,
即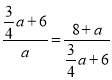 ,
,
解得![]() (舍去),
(舍去),
∴m=![]() .
.
③如图4所示,当DC=OC时,
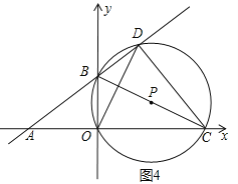
∵OC=m,
∴CD=m,
∴AD=![]() ,
,
∴AC=![]() ,
,
∴8+m=![]() ,
,
解得m=12.
④如图5所示,当OD=OC时,
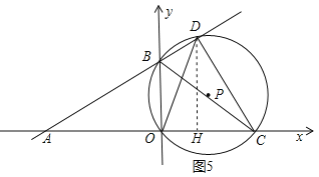
OC=OD=m,
∴AC=8+m,
∴AD=AC×cos∠BAO=![]() ,
,
则AH=AD×cos∠BAO=![]() ,
,
∴OH=AH-8=![]() ,
,
∵DH=AD×sin∠BAO=![]() ,
,
∴![]() ,
,
解得m=±8.
∵m>0
∴m=8
综上所述,m的值为-3或![]() 或12或 8.
或12或 8.
(4)解:如图6所示,连结OQ,
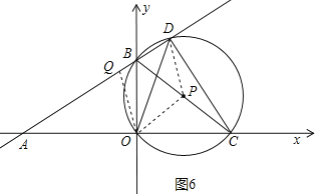
∵PD=DQ,PO=OQ,PD=OP,
∴DQ=DP=PO=OQ,
∴四边形DQOP为菱形,
∴DQ∥PO,
∴∠BOP=∠PBO=∠ABO,
在Rt△BOC中,∠BOC=90°,P为BC中点
∴BP=![]() BC=
BC=![]() BO÷cos∠BOP=5,
BO÷cos∠BOP=5,
∴OQ=5,
设点Q的坐标为(c,![]() ),
),
则OQ=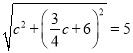 ,
,
∴![]()
∵c=-4时,B、D重合
∴c=-4不符合题意,舍去
∴![]()
∴Q(-![]() ,
,![]() ),
),
∴BQ=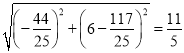 .
.

 阅读快车系列答案
阅读快车系列答案