题目内容
10.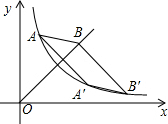 如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,求B点坐标.
如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,求B点坐标.
分析 首先利用反比例函数图象上点的坐标性质得出A′点坐标,再利用平行四边形的性质假设出B点坐标,进而表示出B′点坐标,即可代入反比例函数解析式得出答案.
解答 解:∵反比例函数y=$\frac{k}{x}$(x>0),点A(1,4),
∴k=1×4=4,
∴反比例函数解析式为:y=$\frac{4}{x}$,
∵点A′(4,b)在反比例函数的图象上,
∴4b=4,
解得:b=1,
∴A′(4,1),
∵点B在直线y=x上,
∴设B点坐标为:(a,a),
∵点A(1,4),A′(4,1),
∴A点向下平移3个单位,再向右平移3个单位,即可得到A′点,
∵四边形AA′B′B是平行四边形,
∴B点点向下平移3个单位,再向右平移3个单位,即可得到B′点(a+3,a-3),
∵点B′在反比例函数的图象上,
∴(a+3)(a-3)=4,
解得:a=±$\sqrt{13}$(负数不合题意),
故B点坐标为:($\sqrt{13}$,$\sqrt{13}$).
点评 此题主要考查了反比例函数综合以及平行四边形的性质、平移的性质等知识,根据题意表示出B′点坐标是解题关键.

练习册系列答案
相关题目
19. 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象上到原点O距离最小的点为A,四边形OADC是平行四边形,且点D也在反比例函数y=$\frac{k}{x}$(x<0)图象上,点C的坐标为(1,3),则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象上到原点O距离最小的点为A,四边形OADC是平行四边形,且点D也在反比例函数y=$\frac{k}{x}$(x<0)图象上,点C的坐标为(1,3),则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象上到原点O距离最小的点为A,四边形OADC是平行四边形,且点D也在反比例函数y=$\frac{k}{x}$(x<0)图象上,点C的坐标为(1,3),则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象上到原点O距离最小的点为A,四边形OADC是平行四边形,且点D也在反比例函数y=$\frac{k}{x}$(x<0)图象上,点C的坐标为(1,3),则k的值为( )| A. | -2 | B. | -$\frac{9}{4}$ | C. | -$\frac{8}{3}$ | D. | -3 |
20.若a>b,则下列不等式一定成立的是( )
| A. | ac>bc | B. | -$\frac{1}{2}$a>-$\frac{1}{2}$b | C. | a+1<1+b | D. | 3a>3b |
 如图所示,已知点A(-1,0),B(3,0),C(0,t),且t>0,tan∠BAC=3,抛物线经过A、B、C三点,点P(2,m)是抛物线上一点.
如图所示,已知点A(-1,0),B(3,0),C(0,t),且t>0,tan∠BAC=3,抛物线经过A、B、C三点,点P(2,m)是抛物线上一点.