题目内容
19. 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象上到原点O距离最小的点为A,四边形OADC是平行四边形,且点D也在反比例函数y=$\frac{k}{x}$(x<0)图象上,点C的坐标为(1,3),则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象上到原点O距离最小的点为A,四边形OADC是平行四边形,且点D也在反比例函数y=$\frac{k}{x}$(x<0)图象上,点C的坐标为(1,3),则k的值为( )| A. | -2 | B. | -$\frac{9}{4}$ | C. | -$\frac{8}{3}$ | D. | -3 |
分析 首先设点A的坐标为:(x,y),可得xy=k,由反比例函数y=$\frac{k}{x}$(x<0)的图象上到原点O的距离最小的点为A,可得y=-x,又由将线段OA平移到线段CD,点O的对应点C(1,3)且点D也在反比例函数y=$\frac{k}{x}$(x<0)的图象上,可得点D的坐标为;(x+1,y+3),继而求得点A的坐标,即可求得答案.
解答 解:设点A的坐标为:(x,y),
∴xy=k,
∵点A在第二象限,
∴x<0,y>0,
∵OA2=x2+y2≥2|xy|,
∴当|x|=|y|时,OA2最小,
即当y=-x时,OA最小,
∵将线段OA平移到线段CD,点O的对应点C(1,3)且点D也在反比例函数y=$\frac{k}{x}$(x<0)的图象上,
∴点D的坐标为:(x+1,y+3),
∴(x+1)(y+3)=k,
∴xy+3x+y+3=k,
即3x+y=-3,
∴3x-x=-3,
解得:x=-$\frac{3}{2}$,y=$\frac{3}{2}$,
∴点A的坐标为:(-$\frac{3}{2}$,$\frac{3}{2}$),
∴k=xy=-$\frac{9}{4}$.
故选B.
点评 此题考查了反比例函数的性质、待定系数法求反比例函数的解析式以及几何不等式的应用.此题难度较大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
4.以下列各组长度的线段为边,能够成三角形的是( )
| A. | 8,5,12 | B. | 6,8,15 | C. | 4,6,15 | D. | 8,3,4 |
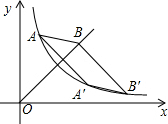 如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,求B点坐标.
如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,求B点坐标.