题目内容
把两个相同的矩形按如图所示的方式叠合起来，若它们的长与宽分别为48cm与36cm，则重叠部分的面积为________cm2．
810
分析：先求出AD的长，再证明△ADE∽△ABC，得出S△ADE=
S△ABC，故重叠部分的面积=
S△ABC．
解答：
解：在RT△ABC中，由勾股定理，得AC=
=60cm，
AD=AC-CD=60-48=12．
在△ADE与△ABC中，∵∠DAE=∠BAC，∠ADE=∠B=90°，
∴△ADE∽△ABC，
∴
=（
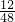）2=（
）2=，
∴S△ADE=S△ABC，
∴重叠部分的面积=S△ABC=×
×48×36=810（cm2）．
点评：本题主要考查了相似三角形的判定与性质，勾股定理，矩形的性质，难度中等．证明△ADE∽△ABC，得出S△ADE=S△ABC是解题的关键．
分析：先求出AD的长，再证明△ADE∽△ABC，得出S△ADE=
S△ABC，故重叠部分的面积=S△ABC．解答：
解：在RT△ABC中，由勾股定理，得AC==60cm，AD=AC-CD=60-48=12．
在△ADE与△ABC中，∵∠DAE=∠BAC，∠ADE=∠B=90°，
∴△ADE∽△ABC，
∴
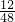=（）2=（）2=，∴S△ADE=
S△ABC，∴重叠部分的面积=
S△ABC=××48×36=810（cm2）．点评：本题主要考查了相似三角形的判定与性质，勾股定理，矩形的性质，难度中等．证明△ADE∽△ABC，得出S△ADE=
S△ABC是解题的关键． 
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
（2012•海门市模拟）把两个相同的矩形按如图所示的方式叠合起来，重叠部分为图中的阴影部分，已知矩形的长与宽分别为4cm与3cm，则重叠部分的面积为
（2012•鼓楼区一模）把两个相同的矩形按如图所示的方式叠合起来，若它们的长与宽分别为48cm与36cm，则重叠部分的面积为
