题目内容
 (2012•鼓楼区一模)把两个相同的矩形按如图所示的方式叠合起来,若它们的长与宽分别为48cm与36cm,则重叠部分的面积为
(2012•鼓楼区一模)把两个相同的矩形按如图所示的方式叠合起来,若它们的长与宽分别为48cm与36cm,则重叠部分的面积为810
810
cm2.分析:先求出AD的长,再证明△ADE∽△ABC,得出S△ADE=
S△ABC,故重叠部分的面积=
S△ABC.
| 1 |
| 16 |
| 15 |
| 16 |
解答: 解:在RT△ABC中,由勾股定理,得AC=
解:在RT△ABC中,由勾股定理,得AC=
=60cm,
AD=AC-CD=60-48=12.
在△ADE与△ABC中,∵∠DAE=∠BAC,∠ADE=∠B=90°,
∴△ADE∽△ABC,
∴
=(
)2=(
)2=
,
∴S△ADE=
S△ABC,
∴重叠部分的面积=
S△ABC=
×
×48×36=810(cm2).
 解:在RT△ABC中,由勾股定理,得AC=
解:在RT△ABC中,由勾股定理,得AC=| AB2+BC2 |
AD=AC-CD=60-48=12.
在△ADE与△ABC中,∵∠DAE=∠BAC,∠ADE=∠B=90°,
∴△ADE∽△ABC,
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
| 12 |
| 48 |
| 1 |
| 16 |
∴S△ADE=
| 1 |
| 16 |
∴重叠部分的面积=
| 15 |
| 16 |
| 15 |
| 16 |
| 1 |
| 2 |
点评:本题主要考查了相似三角形的判定与性质,勾股定理,矩形的性质,难度中等.证明△ADE∽△ABC,得出S△ADE=
S△ABC是解题的关键.
| 1 |
| 16 |

练习册系列答案
相关题目
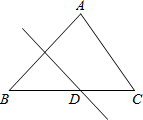 (2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )
(2012•鼓楼区一模)如图,△ABC中,∠ABC=45°,AC=10,对折使点B与点A重合,折痕与BC交于点D,BD:DC=4:3,则DC的长为( )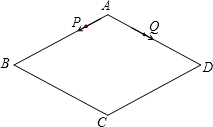 /s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.
/s;点Q沿折线A-D-C-B运动,速度为1.5cm/s.当一点到达终点时,另一点也随即停止运动.若点P、Q同时从点A出发,运动时间为t s.