题目内容
1. 如图,平面直角坐标系的原点O是正方形ABCD的中心,顶点A,B的坐标分别为(1,1),(-1,1),把正方形ABCD绕原点O逆时针旋转45°得正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分所形成的正八边形的边长为2$\sqrt{2}$-2.
如图,平面直角坐标系的原点O是正方形ABCD的中心,顶点A,B的坐标分别为(1,1),(-1,1),把正方形ABCD绕原点O逆时针旋转45°得正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分所形成的正八边形的边长为2$\sqrt{2}$-2.
分析 如图,首先求出正方形的边长、对角线长;进而求出OA′的长;证明△A′MN为等腰直角三角形,求出A′N的长度;同理求出D′M′的长度,即可解决问题.
解答 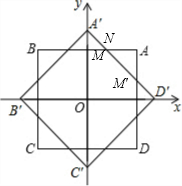 解:如图,由题意得:
解:如图,由题意得:
正方形ABCD的边长为2,
∴该正方形的对角线长为2$\sqrt{2}$,
∴OA′=$\sqrt{2}$;而OM=1,
∴A′M=$\sqrt{2}$-1;
由题意得:∠MA′N=45°,∠A′MN=90°,
∴∠MNA′=45°,
∴MN=A′M=$\sqrt{2}-1$;
由勾股定理得:A′N=2-$\sqrt{2}$;
同理可求D′M′=2-$\sqrt{2}$,
∴NM'=2-(4-2$\sqrt{2}$)=2$\sqrt{2}$-2,
∴正八边形的边长为2$\sqrt{2}$-2.
点评 该题主要考查了旋转变换的性质、正方形的性质、勾股定理等几何知识点及其应用问题;应牢固掌握旋转变换的性质、正方形的性质等几何知识点,这是灵活运用、解题的基础和关键.

练习册系列答案
相关题目
11.正六边形的边心距是$\sqrt{3}$,则它的边长是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
9.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为( )
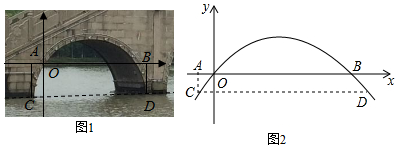

| A. | 16$\frac{9}{40}$米 | B. | $\frac{17}{4}$米 | C. | 16$\frac{7}{40}$米 | D. | $\frac{15}{4}$米 |
6.方程$\frac{{x}^{2}-1}{x+1}$=0的解是( )
| A. | 1或-1 | B. | -1 | C. | 0 | D. | 1 |
13.-2的倒数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
10.若反比例函数y=$\frac{k}{x}$的图象经过点(2,-1),则该反比例函数的图象在( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
11.今年5月,在成都举行的世界机场城市大会上,成都新机场规划蓝图首次亮相,新机场建成后,成都将成为继北京、上海之后,国内第三个拥有双机场的城市,按照远期规划,新机场将建的4个航站楼的总面积约为126万平方米,用科学记数法表示为( )
| A. | 126×104 | B. | 1.26×105 | C. | 1.26×106 | D. | 1.26×107 |