题目内容
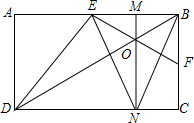 如图,四边形ABCD是矩形,点E是边AB上的点,过点E作DE的垂直线交对角线BD于点O,交边BC于点F.
如图,四边形ABCD是矩形,点E是边AB上的点,过点E作DE的垂直线交对角线BD于点O,交边BC于点F.(1)△ADE与△BEF相似吗?说明理由;
(2)过点O作AB的垂线交AB于点M,交CD于点N,连接NB、NE,若NB=NE,证明:线段BO是△BEF的EF边上的中线;
(3)在(2)的条件下,若点E是AB的中点,且AB=4,求线段DO的长.
考点:相似形综合题
专题:
分析:(1)根据矩形的性质,可得∠A=∠ABC=90°,根据同角的余角相等,可得∠ADE=∠BEF,根据两个角相等的三角形相似,可得答案;
(2)根据等腰三角形的性质,可得BM与EM的关系,根据三角形中位线的性质,可得答案;
(3)根据相似三角形的判定与性质,可得BO与OD的关系,根据三角形中位线的性质,可得EG与AD的关系,BG与BD的关系,根据平行四边形的判定与性质,可得BF与EG的关系,根据相似三角形的性质,可得
=
,根据比例的性质,可得AD的长,根据勾股定理,可得BD的长,根据按比例分配,可得答案.
(2)根据等腰三角形的性质,可得BM与EM的关系,根据三角形中位线的性质,可得答案;
(3)根据相似三角形的判定与性质,可得BO与OD的关系,根据三角形中位线的性质,可得EG与AD的关系,BG与BD的关系,根据平行四边形的判定与性质,可得BF与EG的关系,根据相似三角形的性质,可得
| AD |
| BE |
| AE |
| BF |
解答:解:(1)△ADE∽△BEF,理由如下:
∵ABCD是矩形,
∴∠A=∠ABC=90°,
∴∠ADE+∠AED=90°.
∵EF⊥DE,
∴∠AED+∠BEF=90°,
∴∠ADE=∠BEF,
∴△ADE∽△BEF.
(2)∵NB=NE,NM⊥BE,
∴BM=EM,MN∥BC,
∴MO是△EBF的中位线,
∴OE=OF,
∴BO是△BEF的边EF上的中线.
(3)∵AB=4,E为AB的中点,
∴BE=
AB=2,BM=
BE=1.
∴CN=BM=1,DN=3.
∵BM∥DN,
∴△OBM∽△ODN,
∴
=
=
.
过E作EG⊥AB交BD于G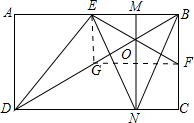 ,
,
∵E为AB中点,
∴EG是△ABD的中位线,
∴G为BD中点,
∴BG=
BD,EG=
AD,
∴BO=GO,
又∵OE=OF,
∴四边形EGFB是平行四边形.
∴BF=EG=
AD.
∵△ADE∽△BEF,
∴
=
,
∴AD•BF=AE•BE,即
AD2=2×2
AD=2
,
BD=
=
=2
∴OD=
BD=
.
∵ABCD是矩形,
∴∠A=∠ABC=90°,
∴∠ADE+∠AED=90°.
∵EF⊥DE,
∴∠AED+∠BEF=90°,
∴∠ADE=∠BEF,
∴△ADE∽△BEF.
(2)∵NB=NE,NM⊥BE,
∴BM=EM,MN∥BC,
∴MO是△EBF的中位线,
∴OE=OF,
∴BO是△BEF的边EF上的中线.
(3)∵AB=4,E为AB的中点,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴CN=BM=1,DN=3.
∵BM∥DN,
∴△OBM∽△ODN,
∴
| BO |
| DO |
| BM |
| DN |
| 1 |
| 3 |
过E作EG⊥AB交BD于G
 ,
,∵E为AB中点,
∴EG是△ABD的中位线,
∴G为BD中点,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
∴BO=GO,
又∵OE=OF,
∴四边形EGFB是平行四边形.
∴BF=EG=
| 1 |
| 2 |
∵△ADE∽△BEF,
∴
| AD |
| BE |
| AE |
| BF |
∴AD•BF=AE•BE,即
| 1 |
| 2 |
AD=2
| 2 |
BD=
| AD2+AB2 |
| 8+16 |
| 6 |
∴OD=
| 3 |
| 4 |
3
| ||
| 2 |
点评:本题考查了相似形综合题,利用了相似三角形的判定;等腰三角形的性质,三角形的中位线;相似三角形的性质三角形的中位线,勾股定理,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)请找出该残片所在圆的圆心O的位置(保留画图痕迹,不必写画法);
(1)请找出该残片所在圆的圆心O的位置(保留画图痕迹,不必写画法);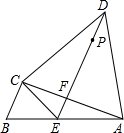 某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.
某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.