题目内容
9. 如图,OA、OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C、D,连接CB、AB.
如图,OA、OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C、D,连接CB、AB.求证:∠ABC=2∠CBO.
分析 连接OC、AC,如图,根据线段垂直平分线的性质得OC=AC,则可判断△OAC是等边三角形,所以∠AOC=60°,于是根据圆周角定理得到∠ABC=$\frac{1}{2}$∠AOC=30°,然后在△BOC中,由于∠BOC=∠AOC+∠AOB=150°,根据三角形内角和可计算出∠CBO=15°,所以∠ABC=2∠CBO.
解答 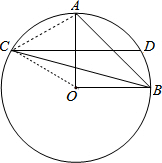 证明:连接OC、AC,如图,
证明:连接OC、AC,如图,
∵CD垂直平分OA,
∴OC=AC.
∴OC=AC=OA,
∴△OAC是等边三角形,
∴∠AOC=60°,
∴∠ABC=$\frac{1}{2}$∠AOC=30°,
在△BOC中,∠BOC=∠AOC+∠AOB=150°,
∵OB=OC,
∴∠CBO=15°,
∴∠ABC=2∠CBO.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了线段垂直平分线的性质和等边三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.计算(a3)2•a2的结果是( )
| A. | a7 | B. | a8 | C. | a10 | D. | a11 |
14.将6.18×10-3化为小数是( )
| A. | 0.000618 | B. | 0.00618 | C. | 0.0618 | D. | 0.618 |
1.已知△ABC∽△A′B′C′且$\frac{AB}{A'B'}=\frac{1}{2}$,则S△ABC:S△A'B'C′为( )
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:1 |
18.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,方差分别是s2甲=0.82,s2乙=1.11,s2丙=0.53,s2丁=1.58,在本次测试中,成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
19.已知∠α=35°,则∠α的补角的度数是( )
| A. | 55° | B. | 65° | C. | 145° | D. | 165° |
