题目内容
n个小杯中依次盛有b1，b2，…bn克糖水，并且分别含糖a1，a2…，an克．若这n杯糖水的浓度相同，则有连等式
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
现将这n杯糖水合到一个大空杯中，则合杯糖水的浓度与各小杯糖水的浓度还是一样的．
这个尽人皆知的事实，说明一个数学定理----一等比定理：
若
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
| a1+a2+…+an |
| b1+b2+…+bn |
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
若这n杯糖水的浓度互不相同，不妨设
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
现将这n杯糖水合到一个大空杯中，则合杯糖水的浓度一定大于
这个尽人皆知的事实，又说明了一个数学定理-----不等比定理：
若
| a1 |
| b1 |
| a2 |
| b2 |
| an |
| bn |
分析：本题主要考查利用生活常识来解决数学问题．
解答：解：合到一个大空杯中时，大空杯中糖水的浓度一定大于原来各小杯中最小的浓度，而小于各小杯中最大的浓度；
而混合后的浓度=总糖量÷总溶液．那么就可得到相应的不等比性质．
由此可得：
这n杯糖水合到一个大空杯中，则合杯糖水的浓度一定大于
，且小于
．
＜
＜
．
而混合后的浓度=总糖量÷总溶液．那么就可得到相应的不等比性质．
由此可得：
这n杯糖水合到一个大空杯中，则合杯糖水的浓度一定大于
| a1 |
| b1 |
| an |
| bn |
| a1 |
| b1 |
| a1+a2+…+an |
| b1+b2+…+bn |
| an |
| bn |
点评：主要培养学生的观察能力和空间想象能力．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
．
，则
．
，
．
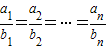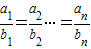，则
．
，
，则 ．
．
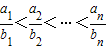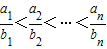，则
．
，
，则 ．