题目内容
锐角三角形ABC中，∠A=30°．以BC边为直径作圆，与AB，AC分别交于D，E，连接DE，把三角形ABC分成三角形ADE与四边形BDEC，设它们的面积分别为S1，S2，则S1：S2=________．
3：1
分析：由于BC是直径，连BE，可得BE⊥AC，再过点D作DF⊥AC，则△ABC与△ADE的面积可用线段表示出来，进而再由割线定理以及30°直角三角形边长之间的关系，通过线段之间的转化，即可求解．
解答：
解：过点D作DF⊥AC，连接BE，
由割线定理可得AD•AB=AE•AC，
∵∠A=30°，∴BE=
AB，DF=AD，
S△ABC=AC•BE，
S1=AE•DF，
=
=
•
=•
=•
=
=
，
∴
=
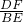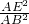=3．
故答案为3：1．
点评：本题主要考查了割线定理以及三角形面积的计算问题，能够通过线段之间的转化求解一些简单的问题，对割线定理以及三角形面积的计算应熟练掌握．
分析：由于BC是直径，连BE，可得BE⊥AC，再过点D作DF⊥AC，则△ABC与△ADE的面积可用线段表示出来，进而再由割线定理以及30°直角三角形边长之间的关系，通过线段之间的转化，即可求解．
解答：
解：过点D作DF⊥AC，连接BE，由割线定理可得AD•AB=AE•AC，
∵∠A=30°，∴BE=
AB，DF=AD，S△ABC=
AC•BE，S1=
AE•DF，==•=•=•==，∴
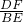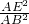==3．故答案为3：1．
点评：本题主要考查了割线定理以及三角形面积的计算问题，能够通过线段之间的转化求解一些简单的问题，对割线定理以及三角形面积的计算应熟练掌握．
练习册系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
16、锐角三角形ABC中，高AD和BE交于点H，且BH=AC，则∠ABC=
如图，在锐角三角形ABC中，AD⊥BC，AD=12cm，AB=13cm，BC=14cm，则AC的长为（ ）| A、12cm | B、13cm | C、14cm | D、15cm |
如图，在锐角三角形ABC中，AD、CE分别是边BC、AB上的高，垂足分别是D、E，AD、CE相交于点O，若∠B=60°，则∠AOE的度数是（ ）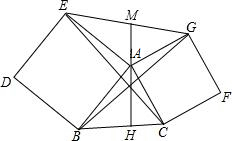
（2013•齐齐哈尔）在锐角三角形ABC中，AH是BC边上的高，分别以AB、AC为一边，向外作正方形ABDE和ACFG，连接CE、BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE ②BG⊥CE ③AM是△AEG的中线 ④∠EAM=∠ABC，其中正确结论的个数是（ ）
在锐角三角形ABC中，AB=4