题目内容
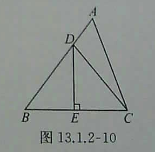
如图所示,角BAC=90°,AD垂直BC,垂足为D,BE平分角ABC,交AC于E,交AD于F,试判断,三角形AEF的形状,并说明理由。解析:是等腰三角形,只要证明出来AF=AE,就行了 补充:
∵ BE平分∠ABC
∴∠ABE=∠CBE
∵ AD⊥BC,
∴ ∠ADB=∠BAC=90°
在 △ABE和△DBF 中
∵∠ABE=∠DBF ∠BAE=∠BDF=90°
∴ △ABE≌△DBF
∴∠AEB=∠BFD(也可以用内角和来证,两对内角相等,另一对内角也相等)
∵ ∠BFD ∠AFE 是对顶角
∴ ∠BFD = ∠AFE
∴ ∠AFE =∠角AEF(角AEF就是角AEB,然后等量代换)
∴△AEF是等腰三角形

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目