题目内容
4．观察：a1=2×20+2；a2=2×21+22；a3=2×22+23；a4=2×23+24；…，请根据你猜想的规律写出an=2n+1．（n为正整数，注意填最简结果）
分析 根据给定等式的变化找出变化规律“an=2n-1”，此题得解．
解答 解：观察，发现规律：a1=2×20+2，a2=2×21+22，a3=2×22+23，a4=2×23+24，…，
∴an=2×2n-1+2n=2n+2n=2n-1．
故答案为：2n-1．
点评 本题考查了规律型中数字的变化类，根据等式的变化找出变化规律是解题的关键．
练习册系列答案
相关题目
12．用反证法证明“若a＞b＞0，则a2＞b2”，应假设（ ）
| A． | a2＜b2 | B． | a2=b2 | C． | a2≤b2 | D． | a2≥b2 |
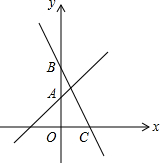如图，已知函数y=x+2的图象与y轴交于点A，一次函数y=kx+b的图象经过点B（0，4）且与x轴及y=x+2的图象分别交于点C、D，点D的坐标为（$\frac{2}{3}$，n）．