题目内容
16.如图,AC⊥l于点C,BD⊥l于点D,且AC=5,BD=11,CD=12.(1)在直线l上找一点M,使MA=MB,求点M到点D的距离.
(2)在直线l上找一点N,使NA+NB最小,求出这个最小值.

分析 (1)根据线段垂直平分线的性质做出线段AB的垂直平分线进而得出与直线l的交点M,根据勾股定理即可得到结论;
(2)如图2,作A的对称点E,连接BE交CD于N,则此时NA+NB最小,即BE=AN+BN,过E作EF⊥BD交BD的延长线于F,根据勾股定理即可得到结论.
解答 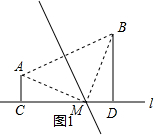 解:(1)如图1,连接AB,作AB的垂直平分线交CD于M,则点M即为所示,
解:(1)如图1,连接AB,作AB的垂直平分线交CD于M,则点M即为所示,
∵AC=5,BD=11,CD=12,
∴CM=12-DM,
∵AC⊥l于点C,BD⊥l于点D,
∴AC2+CM2=DM2+BD2,
即52+(12-DM)2=DM2+112,
∴DM=$\frac{37}{6}$;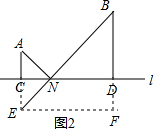
(2)如图2,作A的对称点E,连接BE交CD于N,则此时NA+NB最小,即BE=AN+BN,
过E作EF⊥BD交BD的延长线于F,
∴BF=11+5=16,EF=CD=12,
∴BE=$\sqrt{E{F}^{2}+B{F}^{2}}$=20,
∴这个最小值是20.
点评 此题主要考查了线段垂直平分线的作法,轴对称-最短路径问题,勾股定理,正确的作出图形是解题的关键.

练习册系列答案
相关题目
6.已知反比例函数y=$\frac{k}{x}$经过点(-2,3),则下列各点在此反比例函数图象上的是( )
| A. | (2,3) | B. | (-2,-3) | C. | (-3,2) | D. | (3,2) |
7.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如表:
则这四个中,成绩发挥最稳定的是( )
| 选 手 | 甲 | 乙 | 丙 | 丁 |
| 平均数(环) | 9.2 | 9.2 | 9.2 | 9.2 |
| 方差(环2) | 0.35 | 0.15 | 0.25 | 0.27 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
 如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是(2$\sqrt{3}$-3)a≤DE≤$\frac{1}{2}$a..
如图,△ABC是边长为a的等边三角形,将三角板的30°角的顶点与A重合,三角板30°角的两边与BC交于D、E两点,则DE长度的取值范围是(2$\sqrt{3}$-3)a≤DE≤$\frac{1}{2}$a.. 如图,在已知的△ABC中,按一下步骤作图:
如图,在已知的△ABC中,按一下步骤作图: 一个等腰三角形工件,尺寸标注如图,则△ABC的面积为512$\sqrt{21}$mm2.
一个等腰三角形工件,尺寸标注如图,则△ABC的面积为512$\sqrt{21}$mm2. 如图是一个由5个相同的正方体组成的立体图形,它的俯视图是( )
如图是一个由5个相同的正方体组成的立体图形,它的俯视图是( )


