题目内容
4.华丰电子厂计划国庆大假组织230名职工外出旅游,与出租车公司联系,拟用A、B、C三种型号的旅游客车10辆正好使这批职工一人一座.已知使用的这三种型号的旅游客车的座位数和每辆车每天租金如表所示:| 车型号 | 每辆车的座位数 | 每辆车每天的租金(元) |
| A | 10 | 500 |
| B | 20 | 900 |
| C | 30 | 1250 |
(2)设每天租金的总金额为z元.求出z与x之间函数解析式;
(3)你能为华丰电子厂提出租车的方案吗?如能,最多可以提出多少个方案?其中每天租金最少的方案是什么?(要求:提出的方案应符合题目要求,并要有数学依据;其中每天租金最少方案结论中应明确租用A、B、C三种型号的车各多少辆,这时每天租金是多少.)
分析 (1)设租用A型车x辆,B型车y辆,则C型车10-x-y辆,根据用A、B、C三种型号的旅游客车10辆正好使这批职工一人一座,可列出方程组即可求解.
(2)根据总租金=租用A型车的租金+租用B型车的租金+租用C型车的租金列出方程即可;
(3)首先根据租金计算出哪一种旅游客车的人均票价最少,多租票价少的花费最少,且保证尽可能没有空位.
解答 解:(1)设租用A型车x辆,B型车y辆,则C型车10-x-y辆,
根据题意,得10x+20y+30(10-x-y)=230,
整理得,y=-2x+7;
所以y与x之间的函数解析式为y=-2x+7;
(2)设每天租金的总金额为z元.
z=500x+900y+1250(10-x-y)
=500x+900(-2x+7)+1250(10-x+2x-7)
=-50+10050,
所以z与x之间函数解析式为z=-50+10050;
(3)用A种型号旅游客车人均票价为500÷10=50(元),
用B种型号旅游客车人均票价为900÷20=45(元),
用C种型号旅游客车人均票价为1250÷30=$\frac{125}{3}$(元)
∵用C种型号旅游客车人均票价最少,
∴多租C种型号旅游客车租金最少,
∵230÷30=7…2,
∴租C种型号旅游客车6辆,B种型号旅游客车2辆,C种型号旅游客车1辆,此时没有空位,租金最少,最少租金为1250×6+900×2+500×1=9800元.
点评 此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.

练习册系列答案
相关题目
9.下列说法错误的是( )
| A. | 一个非零数与其倒数之积为1 | |
| B. | 一个数与其相反数之商为-1 | |
| C. | 若两个数的商为-1,则这两个数互为相反数 | |
| D. | 若两个数的积为1,则这两个数互为倒数 |
9. 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )
 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点E的坐标是( )| A. | (4,1) | B. | (3,$\frac{4}{3}$) | C. | ($\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{5}-1}{2}$) | D. | ($\sqrt{6}+\sqrt{2}$,$\sqrt{6}-\sqrt{2}$) |
13.下列调查宜抽样调查而不宜普查的是( )
| A. | 调查八年级(下)数学书的排版正确率 | |
| B. | 调查一批飞行员的视力 | |
| C. | 调查宇宙飞船“神舟十号”的零部件 | |
| D. | 调查市民对“马航MH370失联事件”的认识状况 |
 如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.
如图,△ABC中,∠BAC=120°,∠ABC=15°,∠A,∠B,∠C的对边分别是a,b,c,则a:b:c=2$\sqrt{3}$:($\sqrt{6}$-$\sqrt{2}$):2$\sqrt{2}$.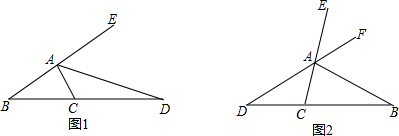
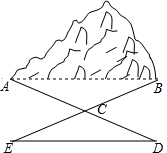 有一座锥形小山,如图,要测量锥形小山两端A、B的距离,先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?
有一座锥形小山,如图,要测量锥形小山两端A、B的距离,先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,你能说说其中的道理吗?