题目内容
如图，量角器的直径与直角三角形ABC的斜边AB重合，射线CP量角器的半圆弧交于点E，若∠ACE=19°，则∠AOE的大小为38
38
度．分析：先根据圆周角定理判断出点C在以点O为圆心，以AB为直径的圆上，再根据圆周角定理进行解答即可．
解答：解：∵∠ACB=90°，
∴点C在以点O为圆心，以AB为直径的圆上，即A、C、B、E共圆，
∵∠ACE=19°，
∴∠AOE=2∠ACE=38°．
故答案为：38．
∴点C在以点O为圆心，以AB为直径的圆上，即A、C、B、E共圆，
∵∠ACE=19°，
∴∠AOE=2∠ACE=38°．
故答案为：38．
点评：本题考查的是圆周角定理，熟知“直径所对的圆周角是直角；同弧所对的圆周角等于所对圆心角的一半”是解答此题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
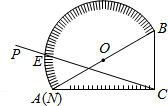（2013•工业园区二模）如图，量角器的直径与直角三角板ABC的斜边AB重合，其中AB=8cm，量角器O刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转，CP与量角器的半圆弧交于点E，第35秒时，点E在量角器上对应划过的
（2013•兰州）如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第24秒，点E在量角器上对应的读数是
（2012•咸宁）如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转，CP与量角器的半圆弧交于点E，第35秒时，点E在量角器上对应的读数是