Question

如图，AB是⊙O的直径，以OA为直径的⊙与⊙O的弦AC相交于点D，DE⊥OC，垂足为E.

（1）求证：AD=DC
（2）DE是⊙的切线吗？说明理由.

Answer 1

（1）通过证明AO是⊙的直径，∠ADO=90°，即OD⊥AC又∵AO=OC∴AD=DC.（2）可通过证明∠DE=∠DEC=90°，DE是⊙的切线.

解析试题分析：20. (1) 连结OD.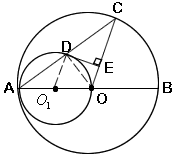

∵AO是⊙的直径，
∴∠ADO=90°，即OD⊥AC，        
又∵AO=OC
∴AD=DC.                  
（2）证明：DE是⊙的切线 ，连结D，
由（1）可得AD=DC，又A=O，∴D∥OC，                       
∴∠DE=∠DEC=90°，                  
∴DE是⊙的切线.   
考点：圆
点评：本题难度较低，主要考查学生对圆的知识点综合运用能力。为中考常考题型，要牢固掌握圆的性质定理灵活运用。