题目内容
一个装有进出水管的水池,单位时间内进、出水量都是一定的.已知水池的容积800升,又知单开进水管20分钟可把空水池注满;若同时打开进、出水管,20分钟可把满水池的水放完,现已知水池内有水200升,先打开进水管3分钟,再打开出水管,两管同时开放,直至把水池中的水放完,则能确定反映这一过程中水池的水量q(升)随时间t(分钟)变化的函数图象是
- A.

- B.

- C.

- D.

B
分析:根据实际意义进行图象的判断,注意特殊点的寻找.
解答:因为进水速度是800÷20=40升/分,同时打开进、出水管,20分钟可把满水池的水放完,则出水速度是40升/分,
所以先打开进水管3分钟,水池中有320升的水,两管同时开放,直至把水池中的水放完共用了320÷40=8分钟,故3+8=11,
故选B.
点评:本题主要考查了根据实际意义读图的能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
分析:根据实际意义进行图象的判断,注意特殊点的寻找.
解答:因为进水速度是800÷20=40升/分,同时打开进、出水管,20分钟可把满水池的水放完,则出水速度是40升/分,
所以先打开进水管3分钟,水池中有320升的水,两管同时开放,直至把水池中的水放完共用了320÷40=8分钟,故3+8=11,
故选B.
点评:本题主要考查了根据实际意义读图的能力.要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.

练习册系列答案
相关题目
 有一个装有进出水管的容器,每单位时间进出的水量都是一定的,设从某时刻开始的5分钟内只进水不出水,在随后的15分钟内既进水又出水,在前段过程中得到的时间x(分)与存水量y(升)之间的关系图象如图,若20分钟后只放水不进水,则这段时间内(x>20)y与x之间的函数关系式是( )
有一个装有进出水管的容器,每单位时间进出的水量都是一定的,设从某时刻开始的5分钟内只进水不出水,在随后的15分钟内既进水又出水,在前段过程中得到的时间x(分)与存水量y(升)之间的关系图象如图,若20分钟后只放水不进水,则这段时间内(x>20)y与x之间的函数关系式是( )| A、y=-2x+110(20<x≤55) | ||
| B、y=-2x-110(20<x≤55) | ||
C、y=-2x+95(20<x≤
| ||
| D、y=-2x+110(20<x≤50) |
 28、有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的容量Q(升)随时间t(分)变化的函数关系.
28、有一个装有进出水管的容器,单位时间内进水管与出水管的进出水量均一定,已知容器的容积为600升,图中线段OA与BC,分别表示单独打开一个进水管和单独打开一个出水管时,容器的容量Q(升)随时间t(分)变化的函数关系.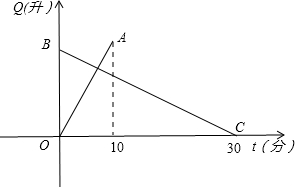
 开一个出水管时,容器内的水量Q(升)随时间t(分)变化的函数关系.根据图象进行以下探究:
开一个出水管时,容器内的水量Q(升)随时间t(分)变化的函数关系.根据图象进行以下探究: