题目内容
 如图,在△ABC中,AB=AC,点D在线段BA的延长线上,且AD=BC,∠BDC=30°,则∠BAC=
如图,在△ABC中,AB=AC,点D在线段BA的延长线上,且AD=BC,∠BDC=30°,则∠BAC=考点:等腰三角形的性质
专题:
分析:作AE⊥DC于E,AF⊥BC于F,利用条件可证得Rt△AEC≌Rt△CFA,得到CE=AF,再结合条件证得四边形AECF是矩形,从而可求得∠BAC.
解答: 解:作AE⊥DC于E,AF⊥BC于F,
解:作AE⊥DC于E,AF⊥BC于F,
∵∠D=30°,
∴AE=
AD,
∵AB=AC,AF⊥BC,
∴BF=CF=
BC,
∵AD=BC,
∴AE=CF,
又∵∠AEC=∠CFA=90°,AC=CA
在△AEC和△CFA中,
,
∴Rt△AEC≌Rt△CFA(HL),
∴CE=AF,
又∵AE=CF,∠AFC=90°,
∴四边形AECF是矩形,
∴∠ECF=90°,
则∠B=60°,
∵AB=AC,
∴△ABC是等边三角形,
∴∠BAC=60°,
故答案为:60°.
 解:作AE⊥DC于E,AF⊥BC于F,
解:作AE⊥DC于E,AF⊥BC于F,∵∠D=30°,
∴AE=
| 1 |
| 2 |
∵AB=AC,AF⊥BC,
∴BF=CF=
| 1 |
| 2 |
∵AD=BC,
∴AE=CF,
又∵∠AEC=∠CFA=90°,AC=CA
在△AEC和△CFA中,
|
∴Rt△AEC≌Rt△CFA(HL),
∴CE=AF,
又∵AE=CF,∠AFC=90°,
∴四边形AECF是矩形,
∴∠ECF=90°,
则∠B=60°,
∵AB=AC,
∴△ABC是等边三角形,
∴∠BAC=60°,
故答案为:60°.
点评:本题主要考查等腰三角形的性质及矩形的判定和性质,构造三角形全等证明四边形AECF是矩形是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
在单项式-a2bc中,下列说法正确的是( )
| A、系数是0,次数是2 |
| B、系数是-1,次数是2 |
| C、系数是1,次数是4 |
| D、系数是-1,次数是4 |
 如图所示,菱形ABCD的对角线相交于点O,E、F在线段BD上,且BE=DF,判断四边形AECF是不是中心对称图形?如果不是,请说明理由;如果是,求出对称中心.
如图所示,菱形ABCD的对角线相交于点O,E、F在线段BD上,且BE=DF,判断四边形AECF是不是中心对称图形?如果不是,请说明理由;如果是,求出对称中心.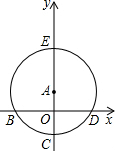 如图,在直角坐标系中,以点A(0,1)为圆心,
如图,在直角坐标系中,以点A(0,1)为圆心,