题目内容
点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为
- A.60°
- B.90°
- C.120°
- D.150°
C
分析:根据角平分线的逆定理求出O是三角形的角平分线的交点,再利用三角形内角和等于180度求解.
解答:连接OA,OB,OC,
∵点O是△ABC内一点,且点O到三边的距离相等,
∴OA、OB、OC分别平分∠BAC、∠ABC、∠ACB,
∵∠BAC=60°,∴∠ABC+∠ACB=120°,
∴∠OBC+∠OCB=120÷2=60°,
∴∠BOC=180-60=120°.
故选C.
点评:本题主要考查角平分线的逆定理,同时综合考查了三角形内角和与角平分线的定义.
分析:根据角平分线的逆定理求出O是三角形的角平分线的交点,再利用三角形内角和等于180度求解.
解答:连接OA,OB,OC,
∵点O是△ABC内一点,且点O到三边的距离相等,
∴OA、OB、OC分别平分∠BAC、∠ABC、∠ACB,
∵∠BAC=60°,∴∠ABC+∠ACB=120°,
∴∠OBC+∠OCB=120÷2=60°,
∴∠BOC=180-60=120°.
故选C.
点评:本题主要考查角平分线的逆定理,同时综合考查了三角形内角和与角平分线的定义.

练习册系列答案
相关题目
 16、如图点P是∠ABC内一点画图:
16、如图点P是∠ABC内一点画图: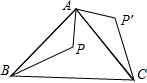 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP= 22、如图,点D是△ABC内一点,点E是△ABC外的一点,且∠1=∠2,∠3=∠4,图中有与∠ACB相等的角吗?如果有,请找出来,并说明理由.
22、如图,点D是△ABC内一点,点E是△ABC外的一点,且∠1=∠2,∠3=∠4,图中有与∠ACB相等的角吗?如果有,请找出来,并说明理由. 如图,点O是△ABC内一点,且点O到三边距离相等,∠BOC=132°,则∠A=
如图,点O是△ABC内一点,且点O到三边距离相等,∠BOC=132°,则∠A=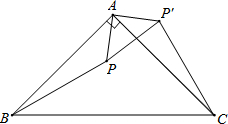 如图,在Rt△ABC中,∠CAB=90°,点P是△ABC内一点,将△ABP绕点A逆时针旋转后能与△ACP′重合,如果AP=5,求PP′的长.
如图,在Rt△ABC中,∠CAB=90°,点P是△ABC内一点,将△ABP绕点A逆时针旋转后能与△ACP′重合,如果AP=5,求PP′的长.