��Ŀ����
����Ŀ������̽��
��![]() ����ͼ�٣���֪������
����ͼ�٣���֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �����㣬��
�����㣬��![]() ������
������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ������
������![]() ��
��![]() ��λ�ù�ϵ����֤����Ľ��ۣ�
��λ�ù�ϵ����֤����Ľ��ۣ�
��![]() ����ͼ�ڣ���֪������
����ͼ�ڣ���֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ����������ͬ���ٶ���
ͬʱ����������ͬ���ٶ���![]() ��
��![]() �������յ�
�������յ�![]() ��
��![]() �˶�������
�˶�������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() �ܳ������ֵ��
�ܳ������ֵ��
������
��![]() ����ͼ����
����ͼ����![]() Ϊ�߳�Ϊ
Ϊ�߳�Ϊ![]() ������
������![]() �ĶԽ��ߣ�
�ĶԽ��ߣ� ![]() ����
����![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ����������ͬ���ٶ���
ͬʱ����������ͬ���ٶ���![]() ��
��![]() ���յ�
���յ�![]() ��
��![]() �˶�������
�˶�������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() �ܳ������ֵ��
�ܳ������ֵ��



���𰸡���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
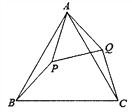
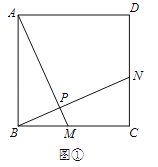
�������������������1�����ۣ�AM��BN��ֻҪ֤����ABM�ա�BCN���ɽ�����⣻
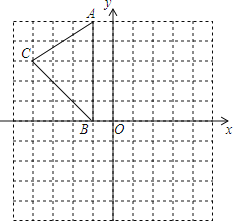
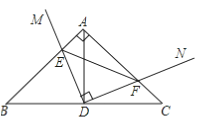
��2����ͼ���У���ABΪб������������ֱ����������AEB����AEB=90������EF��PA��E����EG��PB��G������EP������֤��PA+PB=2EF�����EF�����ֵ���ɽ�����⣻
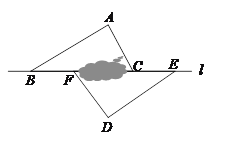
��3����ͼ���У��ӳ�DA��K��ʹ��AK=AB������ABK�ǵȱ������Σ�����PK��ȡPH=PB������֤��PA+PB=PK�����PK�����ֵ���ɽ�����⣻
����������⣺��1�����ۣ�AM��BN������������
��ͼ���У����ı���ABCD�������Σ���AB=BC����ABM=��BCN=90������BM=CN�����ABM�ա�BCN�����BAM=��CBN���ߡ�CBN+��ABN=90�������ABN+��BAM=90�������APB=90������AM��BN��
��2����ͼ���У���ABΪб������������ֱ����������AEB����AEB=90������EF��PA��E����EG��PB��G������EP��
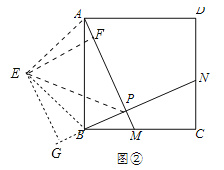
�ߡ�EFP=��FPG=��G=90�������ı���EFPG�Ǿ��Σ����FEG=��AEB=90�������AEF=��BEG����EA=EB����EFA=��G=90�������AEF�ա�BEG����EF=EG��AF=BG�����ı���EFPG�������Σ���PA+PB=PF+AF+PG��BG=2PF=2EF����EF��AE����EF�����ֵ=AE=![]() �����APB�ܳ������ֵ=
�����APB�ܳ������ֵ=![]() ��
��
��3����ͼ���У��ӳ�DA��K��ʹ��AK=AB������ABK�ǵȱ������Σ�����PK��ȡPH=PB��
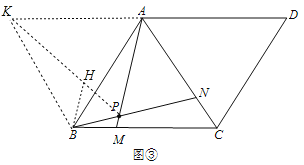
��AB=BC����ABM=��BCN��BM=CN�����ABM�ա�BCN�����BAM=��CBN�����APN=��BAM+��ABP=��CBN+��ABN=60�������APB=120�����ߡ�AKB=60�������AKB+��APB=180������A��K��B��P�ĵ㹲Բ�����BPH=��KAB=60������PH=PB�����PBH�ǵȱ������Σ����KBA=��HBP��BH=BP�����KBH=��ABP����BK=BA�����KBH�ա�ABP����HK=AP����PA+PB=KH+PH=PK����PK��ֵ���ʱ����APB���ܳ��������PK����ABK���Բ��ֱ��ʱ��PK��ֵ������ֵΪ4�����PAB���ܳ����ֵ=![]() ��
��