题目内容
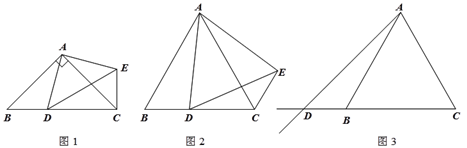
【题目】如图,己知△ABC是等边三角形,点P在△ABC内,点Q在△ABC外,分别连接AP、BP、AQ、CQ,∠ABP=∠ACQ, BP=CQ.
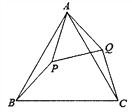
(1)求证:△ABP≌△ACQ;
(2)连接PQ,求证△APQ是等边三角形;
(3)连接P设△CPQ是以![]() PQC为顶角的等腰三角形,且∠BPC=100
PQC为顶角的等腰三角形,且∠BPC=100![]() ,求∠APB的度数.
,求∠APB的度数.
【答案】(1)答案见解析;(2)答案见解析;(3)160°
【解析】试题分析:易证AB=AC,∠BAC=60°,即可证明△ABP≌△ACQ,可得∠BAP=∠CAQ,AP=AQ,即可求得∠PAQ=60°,即可解题.
(1)证明: ∵ △ABC是等边三角形,
∴ AB=AC .
在△ABP和△ACQ中
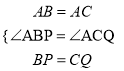 ,
,
∴ △ABP ≌ △ACQ ( SAS ).
(2)证明: ∵ △ABP ≌ △ACQ,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∵ △ABC是等边三角形,
∴ ![]() ,
,
∴ ![]() ,
,
∴ △APQ是等边三角形.
(3)解: 如图示
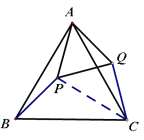
∵ △CPQ是等腰三角形,∠PQC为顶角,
∴ ![]() .
.
设![]() ,
,
![]() =
=![]() .
.
∵ △APQ是等边三角形,
∴ ![]() ,
,
∴ ![]() .
.
∵ △ABP ≌ △ACQ,
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
又∵ ![]()
∴ ![]() ,
,
解得 ![]() ,
,
∴ ![]() .
.
点睛: 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了正三角形的判定,本题中求证△ABP≌△ACQ是解题的关键.

练习册系列答案
相关题目