Question

【题目】如图，在平面直角坐标系中，点，点，其中，，点是轴负半轴上一点，点是在直线与直线之间的一点，连接、，平分，平分，交于，则与之间可满足的数量关系式为______________．

Answer 1

【答案】或

【解析】

分情况讨论：①点P在OB的左边时，根据三角形的内角和定理表示出∠PBO+∠POB的大小，再根据两直线平行、同旁内角互补和角平分线的定义表示出∠NBP+∠NOP，然后在△NBO中，利用三角形的内角和定理列式整理即可得到答案；

②点P在OB的右边时，求出∠CBP+∠AOP+∠BPO=360°，再根据角平分线的定义表示出∠PBN+∠PON，利用四边形的内角和定理列式整理即可得到答案．

解：①如下图，P在OB左侧时，∠BPO=2∠BNO，

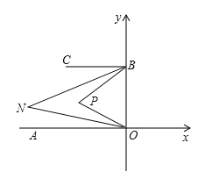
理由如下：在△BPO中，

∵BC∥OA，BN平分∠CBP，ON平分∠AOP，

∴，

在△NOB中，∠BNO=180°-（∠NBP+∠NOP+∠PBO+∠POB），

，

，

，

，

∴；

②如下图，P在OB右侧时，，理由如下：

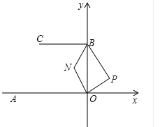
∵BC∥OA，
∴∠CBP+∠AOP+∠BPO=360°，
∵BN平分∠CBP，ON平分∠AOP，

∴，

∴，

在四边形BNOP中，

，

∴

故答案为：或．