题目内容
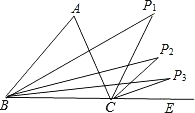
【题目】如图,已知∠A=n°,若P1点是∠ABC和外角∠ACE的角平分线的交点,P2点是∠P1BC和外角∠P1CE的角平分线的交点,P3点是∠P2BC和外角∠P2CE的交点…依此类推,则∠Pn=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
易求得∠P1BC![]() ∠ABC,∠P1CE
∠ABC,∠P1CE![]() ∠ACE,再根据∠ACE=∠A+∠ABC,∠P1CE=∠P1+∠P1BC,即可求得∠P1
∠ACE,再根据∠ACE=∠A+∠ABC,∠P1CE=∠P1+∠P1BC,即可求得∠P1![]() ∠A,根据∠P1
∠A,根据∠P1![]() ∠A,易证∠BP2C
∠A,易证∠BP2C![]() ∠BPC,∠BP3C
∠BPC,∠BP3C![]() ∠BP2C,即可发现规律∠BPnC
∠BP2C,即可发现规律∠BPnC![]() ∠A,即可解题.
∠A,即可解题.
∵BP1平分∠ABC,CP1平分∠ACE,∴∠P1BC![]() ∠ABC,∠P1CE
∠ABC,∠P1CE![]() ∠ACE.
∠ACE.
∵∠ACE=∠A+∠ABC,∠P1CE=∠P1+∠P1BC,∴∠P1![]() ∠A,同理∠BP2C
∠A,同理∠BP2C![]() ∠BP1C,∠BP3C
∠BP1C,∠BP3C![]() ∠BP2C,由此可发现规律∠BPnC
∠BP2C,由此可发现规律∠BPnC![]() ∠A
∠A![]() .
.
故选B.

练习册系列答案
相关题目