题目内容
12.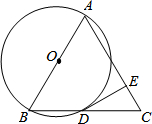 如图,以等腰△ABC的腰AB为直径的⊙O交底边BC于D,DE⊥AC于E,DE是⊙O的切线吗?为什么?
如图,以等腰△ABC的腰AB为直径的⊙O交底边BC于D,DE⊥AC于E,DE是⊙O的切线吗?为什么?
分析 连结OD,如图,根据等腰三角形的性质,由OB=OD得∠B=∠ODB,由AB=AC得∠B=∠C,则∠ODB=∠C,于是可判断OD∥AC,由于DE⊥AC,所以OD⊥DE,则可根据切线的判定定理得到DE是⊙O的切线.
解答 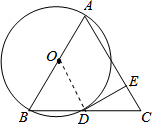 解:DE是⊙O的切线.理由如下:
解:DE是⊙O的切线.理由如下:
连结OD,如图,
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的性质.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
7. 如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
 如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )| A. | 45cm | B. | 59cm | C. | 62cm | D. | 90cm |
17.下列运算中,正确的是( )
| A. | -(m+n)=n-m | B. | (m2n2)3=m6n6 | C. | m3•m2=m6 | D. | n3÷n3=n |
1.下列运算中,正确的是( )
| A. | 2x-x=1 | B. | x+x=2x | C. | (x3)3=x6 | D. | x8÷x2=x4 |
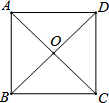 如图,正方形ABCD的对角线交于点O,点F是BC的中点.
如图,正方形ABCD的对角线交于点O,点F是BC的中点.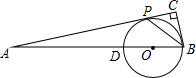 如图,在△ABC中,∠ACB=90°,点P是AC上一点,且BP平分∠ABC,点D是AB上一点,以BD为直径的⊙O经过点P.
如图,在△ABC中,∠ACB=90°,点P是AC上一点,且BP平分∠ABC,点D是AB上一点,以BD为直径的⊙O经过点P.