题目内容
某次围棋比赛采用单循环制(即每个选手必须和其余的选手都比赛一场),共赛了36场,则选手有 名.
考点:一元二次方程的应用
专题:
分析:设选手有x名,则共进行的比赛场数为
场,根据单循环的比赛场数为36场建立方程求出其解即可.
| x(x-1) |
| 2 |
解答:解:设选手有x名,则共进行的比赛场数为
场,由题意,得
=36,
解得:x1=-8(舍去),x2=9,
∴x=9.
故答案为:9.
| x(x-1) |
| 2 |
| x(x-1) |
| 2 |
解得:x1=-8(舍去),x2=9,
∴x=9.
故答案为:9.
点评:本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时根据单循环的比赛场数为36场建立方程是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目

 AD是△ABC的角平分线,如图,那么∠BAC=
AD是△ABC的角平分线,如图,那么∠BAC= 如图,OA,BA分别表示甲、乙两人的运动图象.请根据图象回答下列问题.
如图,OA,BA分别表示甲、乙两人的运动图象.请根据图象回答下列问题. 如图,在正方形ABCD中,若E为AB的中点,则当
如图,在正方形ABCD中,若E为AB的中点,则当 如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于点D,如果BC=10cm,那么△BCD的周长是
如图,在△ABC中,AB=AC=16cm,AB的垂直平分线交AC于点D,如果BC=10cm,那么△BCD的周长是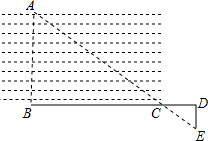 要测量河两岸相对的两点A,B间的距离,先从B处出发,向与AB成90°角的方向走50m到C处,在C处立一根标杆,然后方向不变地继续朝前走10m到D处,在D处转90°,沿DE方向再走17m,到达E处,使A(目标物),C(标杆)与E在同一直线上(如图),那么据此可测得A,B间的距离是
要测量河两岸相对的两点A,B间的距离,先从B处出发,向与AB成90°角的方向走50m到C处,在C处立一根标杆,然后方向不变地继续朝前走10m到D处,在D处转90°,沿DE方向再走17m,到达E处,使A(目标物),C(标杆)与E在同一直线上(如图),那么据此可测得A,B间的距离是