题目内容
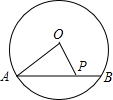 如图,⊙O的半径OA=10cm,弦AB=16cm,P为AB上一动点,则点P到圆心O的最短距离为
如图,⊙O的半径OA=10cm,弦AB=16cm,P为AB上一动点,则点P到圆心O的最短距离为
- A.4cm
- B.5cm
- C.6cm
- D.7cm
C
分析:当OP垂直于AB时,P到圆心O的距离最短,此时由垂径定理得到P为AB的中点,由AB的长求出AP的长,在直角三角形AOP中利用勾股定理即可求出OP的长.
解答: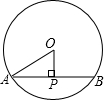 解:当OP垂直于AB时,P到圆心O的距离最短,
解:当OP垂直于AB时,P到圆心O的距离最短,
由垂径定理得到P为AB的中点,即AP= AB=8cm,
AB=8cm,
在Rt△AOP中,OA=10cm,AP=8cm,
根据勾股定理得:OP= =6cm.
=6cm.
故选C.
点评:此题考查了垂径定理,以及勾股定理,熟练掌握垂径定理是解本题的关键.
分析:当OP垂直于AB时,P到圆心O的距离最短,此时由垂径定理得到P为AB的中点,由AB的长求出AP的长,在直角三角形AOP中利用勾股定理即可求出OP的长.
解答:
 解:当OP垂直于AB时,P到圆心O的距离最短,
解:当OP垂直于AB时,P到圆心O的距离最短,由垂径定理得到P为AB的中点,即AP=
 AB=8cm,
AB=8cm,在Rt△AOP中,OA=10cm,AP=8cm,
根据勾股定理得:OP=
 =6cm.
=6cm.故选C.
点评:此题考查了垂径定理,以及勾股定理,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )
如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )| A、10 | B、8 | C、6 | D、4 |
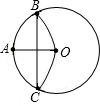 如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )A、6
| ||
B、6
| ||
C、3
| ||
D、3
|
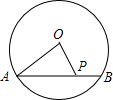 如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为
如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为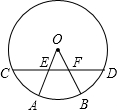 如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.
如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.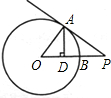 如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,
如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,