题目内容
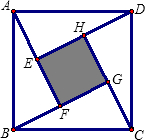
四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图）．如果小正方形面积为4，大正方形面积为74，直角三角形中较小的锐角为θ，那么cosθ的值是 ．
【答案】分析：根据大正方形的面积求得直角三角形的斜边是
，根据大正方形减去小正方形的面积即四个直角三角形的面积和是70，求得两条直角边的乘积是35．再根据勾股定理知直角三角形的两条直角边的平方和等于74，联立解方程组可得两条直角边分别是3，4，则cosθ=7
．
解答：解：根据题意，大正方形边长=
，小正方形的边长=
=2．
∴三角形的面积=（74-4）÷4=
．
设三角形两直角边为a、b，则
ab=
．
又a2+b2=74，
联立解得
，
则cosθ=
=
；
故答案是：
．
点评：本题考查了勾股定理．此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边，进一步运用锐角三角函数的定义求解．
，根据大正方形减去小正方形的面积即四个直角三角形的面积和是70，求得两条直角边的乘积是35．再根据勾股定理知直角三角形的两条直角边的平方和等于74，联立解方程组可得两条直角边分别是3，4，则cosθ=7．解答：解：根据题意，大正方形边长=
，小正方形的边长==2．∴三角形的面积=（74-4）÷4=
．设三角形两直角边为a、b，则
ab=．又a2+b2=74，
联立解得
，则cosθ=
=；故答案是：
．点评：本题考查了勾股定理．此题中根据正方形以及直角三角形的面积公式求得直角三角形的三边，进一步运用锐角三角函数的定义求解．
练习册系列答案
相关题目
正方形．
24、如图所示，把边长为2的正方形剪成四个全等的直角三角形，请你用这四个直角三角形拼成符合下列要求的图形各一个，并标上必要的记号：
19、如图，把边长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形画出符合下列要求的图形（注意：四个三角形要全部用上，互不重叠且不留空隙）．
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形（如图所示）．如果大正方形的面积是49，小正方形的面积4，直角三角形的两直角边长分别为a，b，那么下列结论正确的有（ ）个．
方形拼成一个大的正方形，并且两种方案中直角三角形全等，直角三角形长的直角边长为a，短的直角边长为b．