Question

如图称为“赵爽弦图”，它是由于四个全等的直角三角形与中间的一个小正方形拼成的一个大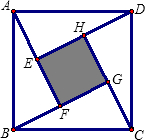正方形．
（1）请说明正方形ABCD∽正方形EFGH；
（2）设∠BAF=α，是否存一个α值，使面积S_{正方形EFGH}=

1

2

S正方形ABCD？如果存在，请求sinα的值；如果不存在，请说明理由．

Answer 1

分析：（1）根据它是由于四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形可以得到：∠BAD=∠FEH，∠ABC=∠EFG，∠BCD=∠FGH，∠CDA=∠GHE和AB=BC=CD=DA，EF=FG=GH=HE，进而可以得到

EF

AB

=

FG

BC

=

GH

CD

=

HE

DA

，从而得到结论
（2）设AB=a，EF=x，据题意可以得到x2=

1

2

a2，即x=

1

2

a．然后再设BF=y，利用勾股定理可以得到（x+y）²+y²=a²，从而解得y=

6 - 2

4

a（负值舍去），然后得到sinα=

BF

AB

=

6 - 2

4

．

解答：解：（1）∵∠BAD=∠FEH，∠ABC=∠EFG，∠BCD=∠FGH，∠CDA=∠GHE，
又AB=BC=CD=DA，EF=FG=GH=HE，
∴

EF

AB

=

FG

BC

=

GH

CD

=

HE

DA

，∴正方形ABCD∽正方形EFGH．（4分）

（2）存在，设AB=a，EF=x，则由条件有x2=

1

2

a2，即x=

1

2

a．（6分）
又设BF=y，则有（x+y）²+y²=a²，
即(

2

2

a+y)2+y2=a2，
化简得：2y2+

2

ay-

1

2

a2=0，（8分）
解得y=

6 - 2

4

a（负值舍去），（9分）∴sinα=

BF

AB

=

6 - 2

4

．（11分）

点评：本题考查了相似多边形的应用、正方形的性质、锐角三角函数的定义及勾股定理的知识，是一道比较复杂的综合题．