题目内容
6.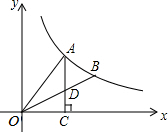 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为( )
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 3 | D. | 4 |
分析 过点B作BE⊥x轴于点E,根据D为OB的中点可知CD是△OBE的中位线,即CD=$\frac{1}{2}$BE,设A(x,$\frac{k}{x}$),则B(2x,$\frac{k}{2x}$),故CD=$\frac{k}{4x}$,AD=$\frac{k}{x}$-$\frac{k}{4x}$,再由△ADO的面积为1求出k的值即可得出结论.
解答  解:过点B作BE⊥x轴于点E,
解:过点B作BE⊥x轴于点E,
∵D为OB的中点,
∴CD是△OBE的中位线,即CD=$\frac{1}{2}$BE.
设A(x,$\frac{k}{x}$),则B(2x,$\frac{k}{2x}$),CD=$\frac{k}{4x}$,AD=$\frac{k}{x}$-$\frac{k}{4x}$,
∵△ADO的面积为1,
∴$\frac{1}{2}$AD•OC=1,$\frac{1}{2}$($\frac{k}{x}$-$\frac{k}{4x}$)•x=1,解得k=$\frac{8}{3}$,
故选:B.
点评 本题考查的是反比例函数系数k的几何意义,熟知反比例函数y=$\frac{k}{x}$图象中任取一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变是解答此题的关键.

练习册系列答案
相关题目
16.不等式组$\left\{\begin{array}{l}{2x+1≤5}\\{x+2>1}\end{array}\right.$的解集是( )
| A. | -1<x<2 | B. | 1<x≤2 | C. | -1<x≤2 | D. | -1<x≤3 |
17.下列四个实数中最大的是( )
| A. | -5 | B. | 0 | C. | π | D. | 3 |
1.一个多边形的外角和是内角和的$\frac{2}{5}$,这个多边形的边数为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
18. 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点P,则k的值为( )| A. | -6 | B. | -5 | C. | 6 | D. | 5 |
 (1)第1列第5行的数是25,第5列第1行的数是17
(1)第1列第5行的数是25,第5列第1行的数是17