题目内容
17.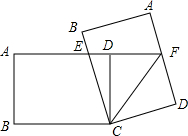 如图,矩形ABCD中,AB=6,AD=8,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′,B′C交AD于E,A′D′交AD延长线于F,当E为AF中点时,△CEF的面积是$\frac{75}{4}$.
如图,矩形ABCD中,AB=6,AD=8,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′,B′C交AD于E,A′D′交AD延长线于F,当E为AF中点时,△CEF的面积是$\frac{75}{4}$.
分析 设ED=x,则AE=8-x,DF=8-2x,根据AAS证得△EGF≌△CDE,得出ED=GF=x,从而求得B′E=AG=x,则CE=8-x,在RT△EDC中,根据勾股定理求得x的值,即可求得EF的长,然后根据三角形面积公式求得即可.
解答 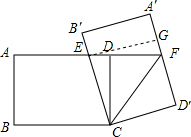 解:作EG⊥A′D′于G,则EG=A′B′=AB=6,B′E=A′G,
解:作EG⊥A′D′于G,则EG=A′B′=AB=6,B′E=A′G,
设ED=x,则AE=8-x,
∵E为AF中点,
∴DF=EF-DE=8-x-x=8-2x,
∴D′F=8-2x,
∴A′F=2x,
∵A′D′∥B′C,
∴∠A′FE=∠DEC,
在△EGF和△CDE中
$\left\{\begin{array}{l}{∠AFE=∠DEC}\\{∠EGF=∠EDC=90°}\\{EG=CD}\end{array}\right.$
∴△EGF≌△CDE(AAS),
∴ED=GF=x,
∴B′E=AG=x,
∴CE=8-x,
在RT△EDC中,CE2=DE2+CD2,
∴(8-x)2=x2+62,解得x=$\frac{7}{4}$,
∴EF=AE=8-x=$\frac{25}{4}$,
∴△CEF的面积是:$\frac{1}{2}$EF•CD=$\frac{1}{2}×$$\frac{25}{4}$×6=$\frac{75}{4}$,
故答案为$\frac{75}{4}$.
点评 本题考查了旋转的性质,三角形全等的判定和性质,勾股定理的应用等,熟练掌握性质定理是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
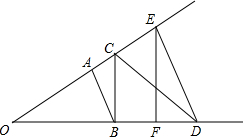 已知A、C、E和B、F、D分别是∠O两边上的点且AB∥ED,BC∥EF,求证:AF∥CD.
已知A、C、E和B、F、D分别是∠O两边上的点且AB∥ED,BC∥EF,求证:AF∥CD.