题目内容
 如图,菱形ABCD中,AB=4,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为
如图,菱形ABCD中,AB=4,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为2
| 3 |
2
.| 3 |
分析:先根据四边形ABCD是菱形可知,AD∥BC,由∠A=120°可知∠ABC=60°,作点N关于直线BD的对称点N′,连接N′M,N′N,则N′M的长即为PM+PN的最小值,由图可知,当点A与点N重合,CM⊥AB时PM+PN的值最小,再在Rt△BCM中利用锐角三角函数的定义求出MC的长即可.
解答: 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AD∥BC,
∵∠A=120°,
∴∠ABC=180°-∠DAB=180°-120°=60°,
作点N关于直线BD的对称点N′,连接N′M,N′N,则N′M的长即为PM+PN的最小值,由图可知,
当点A与点N重合,MN′⊥AB时PM+PN的值最小,
在Rt△BCM中,
∵BC=AB=4,∠ABC=60°,
∴CM=BC•sin∠ABC=4×
=2
.
故答案为:2
.
 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,∴AD∥BC,
∵∠A=120°,
∴∠ABC=180°-∠DAB=180°-120°=60°,
作点N关于直线BD的对称点N′,连接N′M,N′N,则N′M的长即为PM+PN的最小值,由图可知,
当点A与点N重合,MN′⊥AB时PM+PN的值最小,
在Rt△BCM中,
∵BC=AB=4,∠ABC=60°,
∴CM=BC•sin∠ABC=4×
| ||
| 2 |
| 3 |
故答案为:2
| 3 |
点评:本题考查的是轴对称-最短路线问题及菱形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
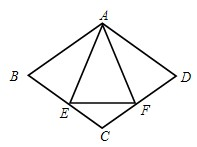 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
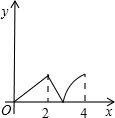
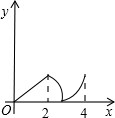
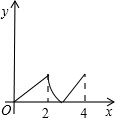
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )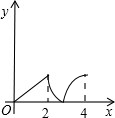
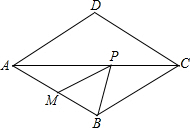 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,