题目内容
已知a=- ,先化简再求代数式
,先化简再求代数式 -
- 的值.
的值.
解:∵a=- ,
,
∴a+1=1- <0,
<0,
 -
- =
= -
- =
= +
+ =
=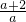 ,
,
当a=- 时,原式=
时,原式= =1-
=1- .
.
分析:先把分子分母分解因式,并约分,求出a+1<0,利用二次根式的性质化简,然后约分,再根据同分母分式的加法进行计算,然后把a的值代入进行计算即可得解.
点评:本题考查了二次根式的化简求值,运用二次根式的性质:a= (a≥0).此题注意借助因式分解的知识达到约分化简的目的.
(a≥0).此题注意借助因式分解的知识达到约分化简的目的.
 ,
,∴a+1=1-
 <0,
<0, -
- =
= -
- =
= +
+ =
=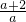 ,
,当a=-
 时,原式=
时,原式= =1-
=1- .
.分析:先把分子分母分解因式,并约分,求出a+1<0,利用二次根式的性质化简,然后约分,再根据同分母分式的加法进行计算,然后把a的值代入进行计算即可得解.
点评:本题考查了二次根式的化简求值,运用二次根式的性质:a=
 (a≥0).此题注意借助因式分解的知识达到约分化简的目的.
(a≥0).此题注意借助因式分解的知识达到约分化简的目的. 
练习册系列答案
相关题目
 ,再求这个代数式的值.
,再求这个代数式的值. ,先化简代数式
,先化简代数式 ,再求这个代数式的值.
,再求这个代数式的值.