题目内容
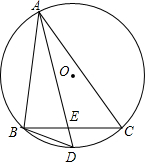 如图,在△ABC的外接圆O中,D是弧BC的中点,AD交BC于点E,连接BD.连接DC,DC2=DE•DA是否成立?若成立,给出证明;若不成立,举例说明.
如图,在△ABC的外接圆O中,D是弧BC的中点,AD交BC于点E,连接BD.连接DC,DC2=DE•DA是否成立?若成立,给出证明;若不成立,举例说明.
分析:欲证DC2=DE•DA,即
=
,只要证明△DEC∽△DCA即可.
| DC |
| DE |
| DA |
| DC |
解答: 解:成立.
解:成立.
连接DC,
∵∠DCB和∠DAB为同弧所对圆周角,
∴∠DCB=∠DAB.
∵∠BAD和∠CAD为等弧所对圆周角,
∴∠BAD=∠CAD.
∴∠DCE=∠DAC.
∵∠CDE=∠ADC,
∴△DEC∽△DCA.
∴
=
.
∴DC2=DE•DA.
 解:成立.
解:成立.连接DC,
∵∠DCB和∠DAB为同弧所对圆周角,
∴∠DCB=∠DAB.
∵∠BAD和∠CAD为等弧所对圆周角,
∴∠BAD=∠CAD.
∴∠DCE=∠DAC.
∵∠CDE=∠ADC,
∴△DEC∽△DCA.
∴
| DC |
| DE |
| DA |
| DC |
∴DC2=DE•DA.
点评:此题主要考查了相似的判定及圆周角定理的综合运用.

练习册系列答案
相关题目
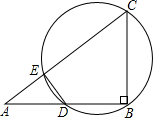 (在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)
(在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)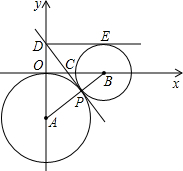 上,过P点作两圆的公切线DP交y轴于D,交x轴于C,
上,过P点作两圆的公切线DP交y轴于D,交x轴于C,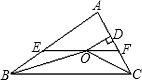 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+ 如图,在△ABC中,BC=12,AB=10,sinB=
如图,在△ABC中,BC=12,AB=10,sinB= 如图,在△ABC中,AB=AC,∠BAC=30°,分别以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°.
如图,在△ABC中,AB=AC,∠BAC=30°,分别以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°. 如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.
如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.