题目内容
如图,P是⊙O上的一个点,⊙P与⊙O的一个交点是E,⊙O的弦AB(或延长线)与⊙P相切,C是切点,AE(或延长线)交⊙P于点F,连接PA、PB,设⊙O的半径为R,⊙P的半径为r(R>r),
(1)如图1,求证:PA•PB=2rR;
(2)如图2,当切点C在⊙O的外部时,(1)中的结论是否成立,试证明之;
(3)探究(图2)已知PA=10,PB=4,R=2r,求EF的长.

(1)证明:连接PO并延长交圆O于H,连接AH、PC,
∵AB是⊙P的切线
∴∠PCB=90°,
∵PH是直径,
∴∠PAH=90°,
∵∠PCB=∠PAH,
∵∠PBC=∠PHA,
∴△PBC∽△PHA,
∴ =
= ,
,
∴PA•PB=2Rr.
(2)结论还成立,
证明:如图:由(1)得:△PBC∽△PHA,
∴ =
= ,
,
∴PA•PB=2Rr.
(3)解:如图2,过P作AE的垂线,垂足是Q,连接PE,
∵PA=10,PB=4,R=2r,
而PA•PB=2Rr,
∴r= ,R=2
,R=2 ,
,
在△PCB和△PQE中,
∠CBP=∠QEP,∠PCB=∠PQE=90°,
∴△PCB∽△PQE,
∴ =
= ,
,
∴PQ= ,
,
∴QE= ,
,
由垂径定理得:EF=2QE= .
.
分析:(1)连接PO并延长交圆O于H,连接AH、PC,证△PBC和△PHA相似,推出比例式即可.
(2)证△PBC和△PAH相似即可推出答案.
(3)过P作AE的垂线,垂足是Q,连接PE,根据(1)的结论求出r,R,证△PCB∽△PQE,求出PQ,根据勾股定理和垂径定理求出即可.
点评:本题考查了对相似三角形的性质和判定,垂径定理,勾股定理,圆周角定理,切线的性质等知识点的连接和运用,解此题的关键是能综合运用这些性质证三角形相似,进而求出线段的长.
∵AB是⊙P的切线
∴∠PCB=90°,
∵PH是直径,
∴∠PAH=90°,
∵∠PCB=∠PAH,
∵∠PBC=∠PHA,
∴△PBC∽△PHA,

∴
 =
= ,
,∴PA•PB=2Rr.
(2)结论还成立,
证明:如图:由(1)得:△PBC∽△PHA,
∴
 =
= ,
,∴PA•PB=2Rr.
(3)解:如图2,过P作AE的垂线,垂足是Q,连接PE,
∵PA=10,PB=4,R=2r,
而PA•PB=2Rr,
∴r=
 ,R=2
,R=2 ,
,在△PCB和△PQE中,
∠CBP=∠QEP,∠PCB=∠PQE=90°,
∴△PCB∽△PQE,
∴
 =
= ,
,∴PQ=
 ,
,∴QE=
 ,
,由垂径定理得:EF=2QE=
 .
.分析:(1)连接PO并延长交圆O于H,连接AH、PC,证△PBC和△PHA相似,推出比例式即可.
(2)证△PBC和△PAH相似即可推出答案.
(3)过P作AE的垂线,垂足是Q,连接PE,根据(1)的结论求出r,R,证△PCB∽△PQE,求出PQ,根据勾股定理和垂径定理求出即可.
点评:本题考查了对相似三角形的性质和判定,垂径定理,勾股定理,圆周角定理,切线的性质等知识点的连接和运用,解此题的关键是能综合运用这些性质证三角形相似,进而求出线段的长.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 25、如图,七巧板是我们祖先的一项卓越创造,在国外被称为“唐图”,由图中标号为“1”、“2”、“3”、“4”、“5”、“6”、“7”的七块板组成.它虽然仅有七块板组成,但用它们可以拼出各种各样的图形.
25、如图,七巧板是我们祖先的一项卓越创造,在国外被称为“唐图”,由图中标号为“1”、“2”、“3”、“4”、“5”、“6”、“7”的七块板组成.它虽然仅有七块板组成,但用它们可以拼出各种各样的图形.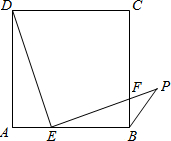 (2012•北京二模)已知:如图,BP是正方形ABCD的一条外角平分线,点E在AB边上,EP⊥ED,EP交BC边于点F.
(2012•北京二模)已知:如图,BP是正方形ABCD的一条外角平分线,点E在AB边上,EP⊥ED,EP交BC边于点F. 如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=
如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=
