Question

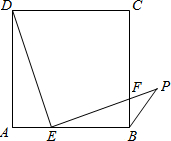（2012•北京二模）已知：如图，BP是正方形ABCD的一条外角平分线，点E在AB边上，EP⊥ED，EP交BC边于点F．
（1）若AE：EB=1：2，求cos∠BEP的值；
（2）请你在图上作直线CM⊥DE，CM与直线AD交于点M，猜想：四边形MEPC的形状有什么特点？证明你的结论．

Answer 1

分析：（1）首先利用已知得出∠BEP=∠BEF=∠ADE，进而得出AE：AB=AE：AD=1：3，即可求出cos∠BEP的值；
（2）首先利用已知得出△ADE≌△DCM，即可得出CM=DE，再得出△BEN∽△BAD，利用三角形全等关系得出△NED≌△BEP，即可得出DE=PE=CM，利用平行四边形的判定得出四边形MEPC是平行四边形．

解答：解：（1）∵EP⊥ED，∴∠DEP=90°．
∴∠BEF=180°-∠DEP-∠AED=90°-∠AED．
又∵∠ADE=90°-∠AED，
∴∠BEP=∠BEF=∠ADE．
∵AE：EB=1：2，
∴AE：AB=AE：AD=1：3．
不妨设AE=1，则AD=3，DE=

10

，cos∠ADE=

3

10

=

3 10

10

．
∴cos∠BEP=

3 10

10

．

（2）作图符合题意，
猜想：四边形MEPC是平行四边形．
证明：∵CM⊥DE，EP⊥ED，∴CM∥EP．
∵∠DCM+∠NDC=90°，∠MDN+∠CDN=90°，
∴∠ADE=∠DCM，
在△ADE和△DCM中，
∵

∠DCM=∠ADE CD=AD ∠CDM=∠A

∴△ADE≌△DCM（ASA），∴CM=DE．
连接BD，作EN∥AD交BD于N，
则△BEN∽△BAD．
又∵四边形ABCD是正方形，BP是外角平分线．
∴EN=EB，∠END=∠EBP=135°．
∵EN∥AD，∴∠NED=∠ADE=∠BEP．
在△NED和△BEP中，
∵

∠END=∠EBP NE=BE ∠NED=∠BEP

，
∴△NED≌△BEP（ASA）．
∴DE=PE=CM．
∴四边形MEPC是平行四边形．
（注：此题证明方法很多，不逐一列举）

点评：此题主要考查了平行四边形的判定和全等三角形的判定与性质和锐角三角函数关系等知识，根据已知得出正确辅助线得出DE=PE=CM是解题关键．