题目内容
6.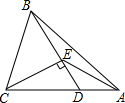 如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.求证:(1)DE=DA;
(2)CE2=AD•AC.
分析 (1)根据直角三角形30度角性质得到DE=$\frac{1}{2}$CD,根据已知条件AD=$\frac{1}{2}$DC,由此不难证明.
(2)先证明∠ECA=∠EAC=∠AED=30°,再证明△DEA∽△ECA即可.
解答 证明:(1)∵CE⊥BD,∠BDC=60°
∴∠ECD=30°,
∴DE=$\frac{1}{2}$CD,又∵CD=2DA,即DA=$\frac{1}{2}$CD,
∴ED=DA.
(2)∵∠EDC=60°=∠DEA+∠DAE,
∵DE=DA,
∴∠DEA=∠DAE=30°,
∵∠ECD=30°,
∴∠ECA=∠EAC=∠AED=30°,
∴EC=EA,
∵∠EAD=∠CAE,∠AED=∠ACE
∴△DEA∽△ECA,
∴$\frac{AE}{AC}$=$\frac{AD}{AE}$,
∴AE2=AD•AC,∴EA=EC,
∴EC2=AD•AC.
点评 本题考查相似三角形的判定和性质、直角三角形30度角的性质、等腰三角形得到和性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
17.下列图形中,轴对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.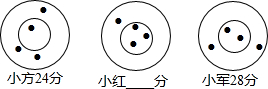 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )| A. | 30分 | B. | 32分 | C. | 33分 | D. | 34分 |
 如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?
如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?
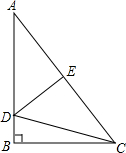 如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$.