题目内容
已知：如图，线段AB、DE表示一个斜靠在墙上的梯子的两个不同的位置，若CB=3m，∠ABC=45°，要使∠EDC=60°，则需BD=________m．
（
）
分析：已知BC，∠ABC=45°，在直角△ABC中根据勾股定理即可计算AB，DE；在直角△ECD中，根据三角函数即可计算CD，BD=BC-CD．
解答：在△ABC中，∠ACB=90°，CB=3m，∠ABC=45°，由勾股定理和等腰直角三角形的性质得AB=3
米，
在△ECD中，∠C=90°，AB=3米，∠EDC=60°，由三角函数得CD=
米，
则BD=BC-CD=（）米，
故答案为：（）．
点评：本题考查了勾股定理在实际生活中的应用，本题中根据梯子长不会变的等量关系求解是解题的关键．
）分析：已知BC，∠ABC=45°，在直角△ABC中根据勾股定理即可计算AB，DE；在直角△ECD中，根据三角函数即可计算CD，BD=BC-CD．
解答：在△ABC中，∠ACB=90°，CB=3m，∠ABC=45°，由勾股定理和等腰直角三角形的性质得AB=3
米，在△ECD中，∠C=90°，AB=3
米，∠EDC=60°，由三角函数得CD=米，则BD=BC-CD=（
）米，故答案为：（
）．点评：本题考查了勾股定理在实际生活中的应用，本题中根据梯子长不会变的等量关系求解是解题的关键．
练习册系列答案
相关题目
已知，如图，线段AB⊥BC，DC⊥BC，垂足分别为点B、C．
2、已知，如图，线段AB上有任一点M，分别以AM，BM为边长作正方形AMFE、MBCD．正方形AMFE、MBCD的外接圆⊙O、⊙O′交于M、N两点，则直线MN的情况是（ ）
已知：如图，线段AB=10cm，点O是线段AB的中点，线段BC=3cm，则线段OC=
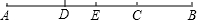
已知：如图，线段AB、DE表示一个斜靠在墙上的梯子的两个不同的位置，若CB=3m，∠ABC=45°，要使∠EDC=60°，则需BD=