题目内容
当x=25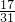 时,代数式|x-1|+|x-2|+|x-3|+…+|x-49|+|x-50|的值为________.
时,代数式|x-1|+|x-2|+|x-3|+…+|x-49|+|x-50|的值为________.
625
分析:根据x的值判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
解答:∵26>x=25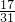 >25,
>25,
∴x-1>0,x-2>0,x-3>0,x-4>0,…x-25>0,x-26<0,x-27<0,…x-50<0,
则原式=x-1+x-2+x-3+x-4+…+x-25+26-x+27-x+28-x+…+50-x=(26+27+…+50)-(1+2+3+…+25)=625.
故答案为:625
点评:此题考查了整式的加减,以及绝对值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.
分析:根据x的值判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
解答:∵26>x=25
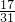 >25,
>25,∴x-1>0,x-2>0,x-3>0,x-4>0,…x-25>0,x-26<0,x-27<0,…x-50<0,
则原式=x-1+x-2+x-3+x-4+…+x-25+26-x+27-x+28-x+…+50-x=(26+27+…+50)-(1+2+3+…+25)=625.
故答案为:625
点评:此题考查了整式的加减,以及绝对值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 、10
、10 ,这辆货车每天行驶的路程为
,这辆货车每天行驶的路程为 .
.
 的代数式填空:
的代数式填空:

 .
.
 、10
、10 ,这辆货车每天行驶的路程为
,这辆货车每天行驶的路程为 .
.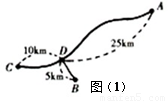
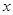 的代数式填空:
的代数式填空: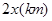
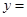
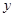 .
.