题目内容
12. 已知关于x的方程x2-2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.
已知关于x的方程x2-2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.(1)试判断△ABC的形状,并说明理由;
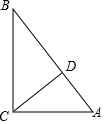
(2)若CD是AB边上的高,AC=2,BD=3,求AD的长.
分析 (1)根据判别式等于0可得出三边的关系,继而可判断出三角形的形状;
(2)结合(1)的结论,可证△ACD∽△ABC得$\frac{AC}{AB}$=$\frac{AD}{AC}$,即$\frac{2}{AD+3}$=$\frac{AD}{2}$,解之可得答案.
解答 解:(1)△ABC是直角三角形,
∵方程x2-2(a+b)x+c2+2ab=0有两个相等的实数根,
∴△=4(a+b)2-4(c2+2ab)=0,
∴a2+b2=c2,
∴△ABC是直角三角形;
(2)∵CD是AB边上的高,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC,
则$\frac{AC}{AB}$=$\frac{AD}{AC}$,即$\frac{2}{AD+3}$=$\frac{AD}{2}$,
解得:AD=1或AD=-4(舍),
故AD=1.
点评 本题考查一元二次方程的根与判别式的关系和相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键

练习册系列答案
相关题目
11.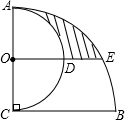 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π-4$ | C. | $3π-2\sqrt{3}$ | D. | 3π-4 |
3.整数8与12的最大公因数是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 24 |
1.下列正比例函数中,y的值随着x值的增大而减小的是( )
| A. | $y=(\sqrt{2}-\sqrt{3})x$ | B. | $y=\frac{1}{5}x$ | C. | y=2x | D. | y=0.2x |
 某同学用所学过的圆与扇形的知识设计了一个问号,如图中阴影部分所示 已知图中大圆半径为4,两个小圆的半径均为2.求图中阴影部分的面积.
某同学用所学过的圆与扇形的知识设计了一个问号,如图中阴影部分所示 已知图中大圆半径为4,两个小圆的半径均为2.求图中阴影部分的面积.