题目内容
 如图所示,一个正比例函数图象与一个一次函数图象相交于点A(3,4),且一次函数的图象与y轴相交于点B.
如图所示,一个正比例函数图象与一个一次函数图象相交于点A(3,4),且一次函数的图象与y轴相交于点B.
(1)求这两个函数的解析式;
(2)求△AOB的面积;
(3)在坐标轴上求一点M使△MOA成为以OA为腰的等腰三角形,求出所有符合条件的点M的坐标.
解:(1)设直线OA为y=kx.
∵y=kx经过点(3,4),
∴3k=4,k= ,
,
∴y= x.
x.
设直线AB为y=ax+b,
∵y=ax+b经过(3,4),(0,-5),
∴ ,
,
解得: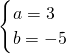 ,⑥
,⑥
∴y=3x-5.
(2)S△AOB= |OB|×3=
|OB|×3= ×5×3=7.5;
×5×3=7.5;
(3)当AO=OM1,AO=5,则M1的坐标为:(5,0),
当AO=AM2,AO=5,则M2的坐标为:(6,0),
当AO=OM3,AO=5,则M3的坐标为:(0,5),
当AO=AM4,AO=5,则M4的坐标为:(0,8),
当AO=OM5,AO=5,则M5的坐标为:(-5,0),
当AO=OM6,AO=5,则M6的坐标为:(0,-5),
故点M的坐标为(6,0)或(5,0)或(-5,0)或(0,5)或(0,8)或(0,-5).
分析:(1)利用待定系数法,将A,B两点分别代入求出即可;
(2)△AOB的高是点A的横坐标3,底边是线段OB的长,所以利用函数解析式求出与y轴交点坐标,从而求出面积,
(3)根据等腰三角形的性质,根据AO为底边或腰分别讨论得出即可.
点评:此题主要考查了用待定系数法解函数解析式和一次函数图象的性质以及等腰三角形的性质,根据等腰三角形的性质分类讨论得出是解题关键.
∵y=kx经过点(3,4),
∴3k=4,k=
 ,
,∴y=
 x.
x.设直线AB为y=ax+b,
∵y=ax+b经过(3,4),(0,-5),
∴
 ,
,解得:
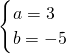 ,⑥
,⑥∴y=3x-5.

(2)S△AOB=
 |OB|×3=
|OB|×3= ×5×3=7.5;
×5×3=7.5;(3)当AO=OM1,AO=5,则M1的坐标为:(5,0),
当AO=AM2,AO=5,则M2的坐标为:(6,0),
当AO=OM3,AO=5,则M3的坐标为:(0,5),
当AO=AM4,AO=5,则M4的坐标为:(0,8),
当AO=OM5,AO=5,则M5的坐标为:(-5,0),
当AO=OM6,AO=5,则M6的坐标为:(0,-5),
故点M的坐标为(6,0)或(5,0)或(-5,0)或(0,5)或(0,8)或(0,-5).
分析:(1)利用待定系数法,将A,B两点分别代入求出即可;
(2)△AOB的高是点A的横坐标3,底边是线段OB的长,所以利用函数解析式求出与y轴交点坐标,从而求出面积,
(3)根据等腰三角形的性质,根据AO为底边或腰分别讨论得出即可.
点评:此题主要考查了用待定系数法解函数解析式和一次函数图象的性质以及等腰三角形的性质,根据等腰三角形的性质分类讨论得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
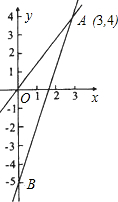 如图所示,一个正比例函数图象与一个一次函数图象交于点(3,4),且一次函数的图象与y轴相交于点B.
如图所示,一个正比例函数图象与一个一次函数图象交于点(3,4),且一次函数的图象与y轴相交于点B.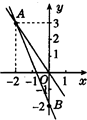 如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.
如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.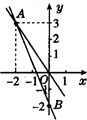 如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.
如图所示,一个正比例函数与一个一次函数的图象相交于点A(-2,3),且一次函数的图象与y轴相交于点B.