题目内容
圆内接四边形ABCD中,四个角的度数比可顺次为( )
| A、4:3:2:1 |
| B、4:3:1:2 |
| C、4:2:3:1 |
| D、4:1:3:2 |
考点:圆内接四边形的性质
专题:
分析:根据圆内接四边形的对角互补即可求解.
解答:解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C=∠B+∠D=180°,
∴∠A与∠C的份数之和=∠B与∠D的份数之和.
故选B.
∴∠A+∠C=∠B+∠D=180°,
∴∠A与∠C的份数之和=∠B与∠D的份数之和.
故选B.
点评:本题考查了圆内接四边形的性质:圆内接四边形的对角互补.

练习册系列答案
相关题目
已知⊙O的半径为2,圆心O到直线l的距离PO=1,则直线l与⊙O的位置关系是( )
| A、相切 | B、相离 |
| C、相交 | D、无法判断 |
 如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )
如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )| A、1个 | B、2个 | C、3个 | D、4个 |
下列命题中,正确的是( )
| A、全等三角形的高相等 |
| B、全等三角形的中线相等 |
| C、全等三角形的角平分线相等 |
| D、全等三角形对应边上的高相等 |
下列命题中,其中的真命题是( )
| A、27的立方根是±3 |
| B、有两边和一个角分别对应相等的两个三角形全等 |
| C、无限小数是无理数 |
| D、两角和其中的对边对应相等的两个三角形全等 |
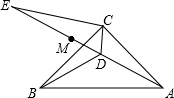 如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA. 在平行四边形ABCD中,AB:AD=3:2,∠ADB=60°,求sinA的值.
在平行四边形ABCD中,AB:AD=3:2,∠ADB=60°,求sinA的值.