题目内容
 如图,已知△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC的长为( )
如图,已知△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC的长为( )分析:首先过点O作OF⊥BC于F,由垂径定理可得BF=CF=
BC,然后由∠BAC=120°,AB=AC,利用等边对等角与三角形内角和定理,即可求得∠C与∠BAC的度数,由BD为⊙O的直径,即可求得∠BAD与∠D的度数,又由AD=6,即可求得BD的长,继而求得BC的长.
| 1 |
| 2 |
解答: 解:过点O作OF⊥BC于F,
解:过点O作OF⊥BC于F,
∴BF=CF=
BC,
∵AB=AC,∠BAC=120°,
∴∠C=∠ABC=
=30°,
∵∠C与∠D是
对的圆周角,
∴∠D=∠C=30°,
∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠ABD=60°,
∴∠OBC=∠ABD-∠ABC=30°,
∵AD=6,
∴BD=
=
=4
,
∴OB=
BD=2
,
∴BF=OB•cos30°=2
×
=3,
∴BC=6.
故选B.
 解:过点O作OF⊥BC于F,
解:过点O作OF⊥BC于F,∴BF=CF=
| 1 |
| 2 |
∵AB=AC,∠BAC=120°,
∴∠C=∠ABC=
| 180°-∠BAC |
| 2 |
∵∠C与∠D是
 |
| AB |
∴∠D=∠C=30°,
∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠ABD=60°,
∴∠OBC=∠ABD-∠ABC=30°,
∵AD=6,
∴BD=
| AD |
| cos30° |
| 6 | ||||
|
| 3 |
∴OB=
| 1 |
| 2 |
| 3 |
∴BF=OB•cos30°=2
| 3 |
| ||
| 2 |
∴BC=6.
故选B.
点评:此题考查了圆周角定理、垂径定理、等腰三角形的性质、直角三角形的性质以及特殊角的三角函数值等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用,注意准确作出辅助线.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
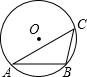 如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为
如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为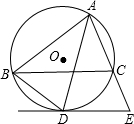 如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E. (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. 如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA.
如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA. 如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.
如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.