题目内容
如图，直角三角板ABC中，∠A=30°，BC=3cm，将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置，沿CB向左平移使B1点落在△ABC的斜边AB上，点B1平移到点B2，则点B由B?B1?B2运动的路程是
- A.（3π+3-
）cm - B.（3π-3+）cm
- C.（
π+3-）cm - D.（π-3+）cm
C
分析：点B由B?B1?B2运动的路程先是一段弧，然后是一直线，所以根据弧长公式可求得弧长，再加上一直线即可．
解答：根据弧长公式可得：
+B1B2．
∵∠A=30°，BC=3cm，
∴AB=6，
根据勾股定理可得：AC=3，
利用相似三角形可得
，
解得B1B2=3-．
所以路程为（π+3-）cm．
故选C．
点评：本题的关键是求线段的长，在这里主要用到了相似三角形的性质．
分析：点B由B?B1?B2运动的路程先是一段弧，然后是一直线，所以根据弧长公式可求得弧长，再加上一直线即可．
解答：根据弧长公式可得：
+B1B2．∵∠A=30°，BC=3cm，
∴AB=6，
根据勾股定理可得：AC=3
，利用相似三角形可得
，解得B1B2=3-
．所以路程为（
π+3-）cm．故选C．
点评：本题的关键是求线段的长，在这里主要用到了相似三角形的性质．
练习册系列答案
相关题目
如图，直角三角板的直角顶点0在直线AB上，斜边CD∥AB，则cosα=
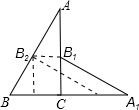如图，直角三角板ABC中，∠A=30°，BC=3cm，将直角三角板绕顶点C按顺时针方向旋转90°至△A1B1C的位置，沿CB向左平移使B1点落在△ABC的斜边AB上，点B1平移到点B2，则点B由B?B1?B2运动的路程是（ ）A、（3π+3-
| ||||
B、（3π-3+
| ||||
C、（
| ||||
D、（
|
如图，直角三角板ABC的斜边AB=12cm，∠A=30°，将三角板ABC绕C顺时针旋转90°至三角板A'B'C'的位置后，再沿CB方向向左平移，使点B'落在原三角板ABC的斜边AB上，则三角板A'B'C'平移的距离为（ ）| A、6cm | ||
| B、4cm | ||
C、（6-2
| ||
D、（4
|
的位置后，再沿CB方向向左平移，使点落在原三角板ABC的斜边AB上，则三角板平移的距离为【 】
）㎝ D.（
）㎝
）cm
）cm