题目内容
9.用适当的方法解方程:x2=2x+35.分析 先把方程化为一般式,然后利用因式分解法解方程.
解答 解:x2-2x-35=0,
(x-7)(x+5)=0,
x-7=0或x+5=0,
所以x1=7,x2=-5.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
20.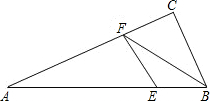 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )| A. | $\frac{5\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 5$\sqrt{3}$ |
14.若代数式xy2与-3xm-1y2n的和是-2xy2,则2m+n的值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1. 如图所示的几何体从上面看得到的平面图形是( )
如图所示的几何体从上面看得到的平面图形是( )
 如图所示的几何体从上面看得到的平面图形是( )
如图所示的几何体从上面看得到的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
18.在0,|-5|,-(-2),-32各数中,负数的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19. 若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
 若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )| A. | a+b>0 | B. | a-b<0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
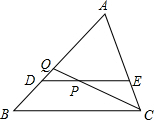 如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.
如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.