题目内容
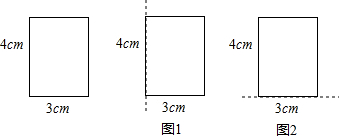
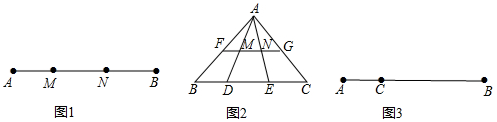
19.定义:如图1,点M、N把线段AB分割成AM,MN和BN,若以AM、MN、BN为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点(1)已知点M、N是线段AB的勾股分割点,若AM=3,MN=4直接写出BN的长;
(2)如图2,在△ABC中,FG∥BC,点D、E是线段BC的勾股分割点,且EC>DE≥BD,连接AD、AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点;
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使C、D是线段AB的勾股分割点(要求简单说明作图过程,保留作图痕迹,画出一种情形即可)
分析 (1)当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;
(2)根据平行线分线段成比例定理得到$\frac{FM}{BD}=\frac{AM}{MD}=\frac{MN}{DE}=\frac{AN}{NE}=\frac{GN}{CE}$=k.根据EC2=BD2+DE2,得到$\frac{1}{{k}^{2}}$GN2=$\frac{1}{{k}^{2}}$FM2+$\frac{1}{{k}^{2}}$MN2,于是得到结论;
(3)①在AB上截取CE=CA;②作AE的垂直平分线,并截取CF=CA;③连接BF,并作BF的垂直平分线,交AB于D;
解答 解:(1)当MN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BM=$\sqrt{M{N}^{2}-A{M}^{2}}=\sqrt{16-9}=\sqrt{7}$,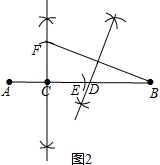
当BN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BN=$\sqrt{M{N}^{2}+A{M}^{2}}=\sqrt{16+9}=5$,
综上,BN=$\sqrt{7}$或5;
(2)证明:∵FG∥BC,
∴$\frac{FM}{BD}=\frac{AM}{MD}=\frac{MN}{DE}=\frac{AN}{NE}=\frac{GN}{CE}$=k.
∴FM=kBD,MN=kDE,GN=kCE.
∴EC2=BD2+DE2,
∴$\frac{1}{{k}^{2}}$GN2=$\frac{1}{{k}^{2}}$FM2+$\frac{1}{{k}^{2}}$MN2,
∴NG2=FM2+MN2.
∴点M,N是线段FG的勾股分割点;
(3)作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图2所示.
点评 本题是三角形综合题目,考查了新定义“勾股分割点”、勾股定理、三角形中位线定理、相似三角形的判定与性质、本题难度较大,综合性强.

 阅读快车系列答案
阅读快车系列答案 如图,下列条件中,不能判定直线l1∥l2的是( )
如图,下列条件中,不能判定直线l1∥l2的是( )| A. | ∠1=∠3 | B. | ∠2+∠4=180° | C. | ∠2=∠3 | D. | ∠4=∠5 |
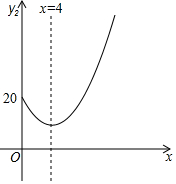 已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:
已知某大型超市今年在销售某种水果时,1~6月份的销售单价y1(元/千克)与时间x(月)的关系如表:| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y1 | 60 | 30 | 20 | 15 | 12 | 10 |
(1)请观察题目中的表格及图象,直接写出y1(元/千克)与时间x(月)的函数关系式及y2(元/千克)与时间x(月)的函数关系式.
(2)求出该种水果今年1~10月哪个月的销售额最大?最大销售额为多少万元?
(3)进入11月后,商场决定将销售单价在取得最大月销售额时的单价的基础上提高2a%,预测月销售量将在取得最大月销售额时的销售量的基础上下降0.5a%,若要使该种水果11月份的销售额达到360万元,求出a的最小整数值(a<100)?(参考数据:$\sqrt{6}$≈2.45;$\sqrt{7}$≈2.65;$\sqrt{8}$≈2.83)
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |