Question

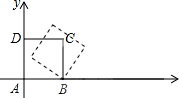如图，边长为1的正方形ABCD 放置在平面直角坐标系中，顶点A与坐标原点O 重合，点B在x轴上．将正方形ABCD沿x轴正方向作无滑动滚动，当点D第一次落在x轴上时，D点的坐标是

 

，D点经过的路径的总长度是

 

；当点D第2014次落在x轴上时，D点经过的路径的总长度是

 

．

Answer 1

考点：弧长的计算,坐标与图形变化-旋转

专题：规律型

分析：由题意可知，将正方形ABCD沿x轴正方向作无滑动滚动，当点D第一次落在x轴上时，D点的坐标是（3，0）；D点经过的路径的总长度=圆心角为90°，半径为

2

的弧长+圆心角为90°，半径为1的弧长；由于正方形ABCD每滚动4次为一个周期，每一个周期点D落在x轴上一次，进而求出点D第2014次落在x轴上时，D点经过的路径的总长度．

解答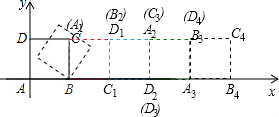：解：如图，正方形ABCD每滚动4次为一个周期，
当点D第一次落在x轴上时，正方形ABCD滚动2次，D点的坐标是（3，0）；
D点经过的路径的总长度是

90π× 2

180

+

90π×1

180

=

2 +1

2

π；
每一个周期中D点经过的路径的总长度是

90π× 2

180

+

90π×1

180

×2=（

2

2

+1）π，
当点D第2014次落在x轴上时，D点经过的路径的总长度是：2013（

2

2

+1）π+

2 +1

2

π=（1007

2

+

4027

2

）π．
故答案为（3，0）；

2 +1

2

π；（1007

2

+

4027

2

）π．

点评：本题考查了旋转的性质，弧长的计算，难度适中．理解题意，得出正方形ABCD每滚动4次为一个周期是解题的关键．